😀前言
在数据结构的学习过程中，二叉搜索树（Binary Search Tree, BST）是一个常见的主题。它不仅具有排序的特性，还为各类算法的实现提供了基础。然而，在某些特定的应用场景中，我们可能需要将二叉搜索树转换为其他形式的数据结构，如双向链表。本文将详细探讨如何将一棵二叉搜索树转换为排序的双向链表，并通过代码实现这一过程。

😀二叉搜索树与双向链表

NowCoder

❤️‍🔥问题描述

给定一棵二叉搜索树，需要将其转换成一个排序的双向链表。双向链表要求如下：

• 每个节点的左指针指向前驱节点，右指针指向后继节点。
• 转换过程中不得创建新的节点，只能调整已有节点的指针。
• 转换后的双向链表中的节点按升序排列，并且返回链表中的第一个节点。

例如，给定的二叉搜索树为：

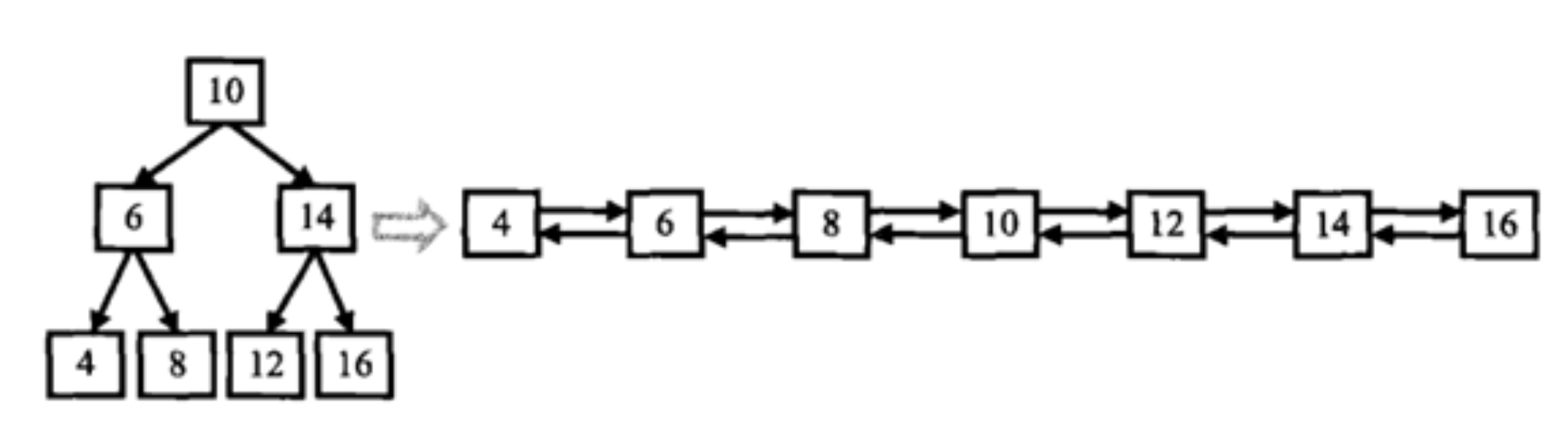
数据范围：输入二叉树的节点数 0≤n≤1000，二叉树中每个节点的值 0≤val≤1000

要求：空间复杂度O(1)（即在原树上操作），时间复杂度 O(n)

😘示例

输入描述：

二叉树的根节点

返回值描述：

双向链表的其中一个头节点。

示例1

输入：{10,6,14,4,8,12,16}

返回值：From left to right are:4,6,8,10,12,14,16;From right to left are:16,14,12,10,8,6,4;

说明：输入题面图中二叉树，输出的时候将双向链表的头节点返回即可。

示例2

输入：{5,4,#,3,#,2,#,1}

返回值：From left to right are:1,2,3,4,5;From right to left are:5,4,3,2,1;

说明：

                    5
                  /
                4
              /
            3
          /
        2
      /
    1
树的形状如上图       

🤔解题思路

将二叉搜索树转换为双向链表的关键在于对树进行中序遍历。中序遍历会按照从小到大的顺序访问树的每个节点，因此可以利用这一特性来构建排序的双向链表。

转换过程的核心步骤如下：

1. 中序遍历： 采用递归的方式，对每个节点进行中序遍历。首先处理左子树，再处理当前节点，最后处理右子树。
2. 指针调整： 在遍历过程中，调整当前节点与前一个节点之间的指针关系，使其形成双向链表。
3. 记录链表头节点： 中序遍历的第一个节点即为双向链表的头节点。

🥰代码实现

以下是用 Java 实现该算法的代码：

private TreeNode pre = null;
private TreeNode head = null;

public TreeNode Convert(TreeNode root) {
    inOrder(root);
    return head;
}

private void inOrder(TreeNode node) {
    if (node == null)
        return;
    
    // 递归遍历左子树
    inOrder(node.left);
    
    // 处理当前节点的前驱与后继关系
    node.left = pre;
    if (pre != null)
        pre.right = node;
    pre = node;
    
    // 记录双向链表的头节点
    if (head == null)
        head = node;
    
    // 递归遍历右子树
    inOrder(node.right);
}

😁代码分析

1. 中序遍历： inOrder 函数实现了二叉树的中序遍历。通过递归的方式，首先处理左子树，再处理当前节点，最后处理右子树。
2. 指针调整： 对于每个被访问的节点，先将其左指针指向前一个访问的节点 pre。如果前一个节点存在，则将其右指针指向当前节点。最后，将 pre 更新为当前节点。
3. 头节点记录： 当 head 为 null 时，意味着当前节点是中序遍历的第一个节点，因此将其记录为双向链表的头节点。

时间与空间复杂度

• 时间复杂度： O(n)，其中 n 为二叉树的节点数。因为我们需要遍历每个节点一次。
• 空间复杂度： O(1)，因为转换是在原树上操作，没有使用额外的存储空间。

😄总结

通过本文的介绍，我们了解了如何将二叉搜索树转换为排序的双向链表。这一过程充分利用了中序遍历的特点，既保留了树中节点的有序性，又通过指针的调整将其转换为双向链表。这一算法不仅简洁高效，还能在实际开发中为各种应用场景提供有效的解决方案。

通过代码的实现，我们可以更直观地理解这一转换过程，并掌握在不同数据结构之间进行转换的技巧。这些知识将在日后的算法学习和实践中发挥重要作用。