排序和动态规划算法的结合通常会用于解决一些特定的问题，以提高算法的效率或简化问题的求解过程。以下是一些结合这两种技术的示例和思路：

1. 最长递增子序列（LIS）：

   • 在求解最长递增子序列问题时，可以先对数列进行排序（如果问题未规定要保留原来元素的相对顺序），再利用动态规划来求解。不过，通常我们可以用动态规划直接在未排序的数组上解决这个问题。
   • 另一种优化方法是使用二分查找结合动态规划来实现 LIS 的求解，以实现 O(n log n) 的时间复杂度，而不是 O(n^2)。

2. 工作调度问题：

   • 在最优工作调度问题中，首先需要对工作按结束时间排序，然后利用动态规划进行决策，选择是否包含某个工作，以最大化利润或最小化时间冲突。

3. 背包问题：

   • 对于某些背包问题，可以对物品进行排序（例如按性价比或体积），然后在动态规划的过程中利用这个排序来构建状态转移方程。

4. 区间选择问题：

   • 在一些涉及区间选择的问题中，通常需要先对区间进行排序（例如按结束时间），然后运用动态规划来选择不重叠的区间，以达到某种最优目标。

5. 其他 combinatorial optimization 问题：

   • 在某些组合优化问题中，排序步骤可以帮助简化可行解的生成过程，从而使得动态规划的计算更加高效。

结合排序和动态规划的关键在于：排序可以帮助我们以某种优先顺序来处理数据，从而使得在动态规划的过程中更容易做出决策或者简化状态空间。因此，这种结合通常可以提高算法的效率和可实现性。我们今天的实例题目就是要这么一个效果，话不多说，直接上题：

​

 2713.矩阵中严格递增的单元格数【困难】

题目：

给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat，你可以选择任一单元格作为 起始单元格 。

从起始单元格出发，你可以移动到 同一行或同一列 中的任何其他单元格，但前提是目标单元格的值 严格大于 当前单元格的值。

你可以多次重复这一过程，从一个单元格移动到另一个单元格，直到无法再进行任何移动。

请你找出从某个单元开始访问矩阵所能访问的 单元格的最大数量 。

返回一个表示可访问单元格最大数量的整数。

示例 1：

​

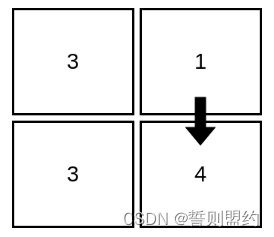
输入：mat = [[3,1],[3,4]]
输出：2
解释：上图展示了从第 1 行、第 2 列的单元格开始，可以访问 2 个单元格。可以证明，无论从哪个单元格开始，最多只能访问 2 个单元格，因此答案是 2 。 

示例 2：

输入：mat = [[1,1],[1,1]]
输出：1
解释：由于目标单元格必须严格大于当前单元格，在本示例中只能访问 1 个单元格。

 示例 3：

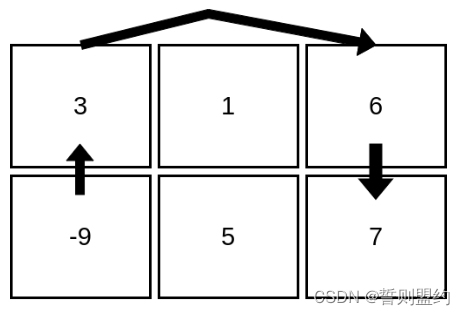
输入：mat = [[3,1,6],[-9,5,7]]
输出：4
解释：上图展示了从第 2 行、第 1 列的单元格开始，可以访问 4 个单元格。可以证明，无论从哪个单元格开始，最多只能访问 4 个单元格，因此答案是 4 。

分析问题：

       这道题旨在寻找一个最大解，可以用动态规划来解，而题意又是让我们顺序移动单元格，只能从小到大的顺序，因此我们可以用一个哈希表来记录每个值所对应的坐标，遍历每个可能的起点。

        在这个过程中，我们可以维护两个数组 rowMax 和 colMax，分别记录每一行和每一列的最大递增长度。初始时，这两个数组的所有元素都为 0。

        对于每个值对应的所有单元格位置，我们按照位置顺序遍历，对于每个位置 (i,j)，我们可以计算出以该位置为终点的最大递增长度为 1+max(rowMax[i],colMax[j])，更新答案，然后更新 rowMax[i] 和 colMax[j]。

代码实现：

class Solution:
    def maxIncreasingCells(self, mat: List[List[int]]) -> int:
        M = len(mat)
        N = len(mat[0])

        # 建立一个哈希表
        value_buckets = defaultdict(list)
        
        for i in range(M):
            for j in range(N):
                value_buckets[mat[i][j]].append((i, j))

        row_best = [0] * M
        col_best = [0] * N
        ans = 0

        for val in sorted(value_buckets.keys()):
            cells = value_buckets[val]
            updates = []
            
            for r, c in cells:
                mx = 1 + max(row_best[r], col_best[c])
                updates.append((r, c, mx))
                ans = max(ans, mx)
            
            for r, c, mx in updates:
                row_best[r] = max(row_best[r], mx)
                col_best[c] = max(col_best[c], mx)
        
        return ans

总结：

代码详解：

        首先，通过 len(mat) 和 len(mat[0]) 分别获取了输入矩阵 mat 的行数 M 和列数 N 。

        然后，创建了一个默认字典 value_buckets 。在接下来的两层循环中，遍历矩阵 mat 的每个元素。对于每个元素的值，将其对应的坐标 (i, j) 添加到 value_buckets 中以该值为键的列表中。

        接着，创建了两个列表 row_best 和 col_best ，分别用于记录每行和每列的最佳值，并初始化为全 0 。还初始化了一个变量 ans 用于保存最终的结果，并初始化为 0 。

        之后，对 value_buckets 中的键（即矩阵中的值）进行排序。对于每个排序后的键值 val ，获取对应的坐标列表 cells 。然后创建一个空列表 updates 用于保存后续的更新信息。

        在遍历 cells 中的每个坐标 (r, c) 时，计算当前位置能达到的最大值 mx ，它等于 1 加上 row_best[r] 和 col_best[c] 中的最大值。将 (r, c, mx) 添加到 updates 列表中，并更新 ans 为 ans 和 mx 中的最大值。

        最后，再次遍历 updates 列表，更新 row_best[r] 和 col_best[c] 为它们自身和 mx 中的最大值。

        最终，方法返回 ans ，即矩阵中按照特定规则能达到的最大结果值。

主要考查内容：

1. 对二维列表的遍历和操作。
2. 使用默认字典 defaultdict 来根据值存储坐标。
3. 对值进行排序，并基于排序后的结果进行一系列计算和更新操作。
4. 维护两个分别记录每行和每列最佳值的列表 row_best 和 col_best 。

通过这段代码可以学到：

1. 如何有效地处理二维数组中的数据。
   • 例如通过两层循环遍历二维数组的每个元素。
2. 运用 defaultdict 来根据特定的值组织数据。
   • 方便后续按照值的顺序进行处理。
3. 结合排序和逐步更新的策略来解决复杂的最值问题。
   • 通过比较和更新 row_best 和 col_best 来获取最终的最大结果。

“千金纵买相如赋，脉脉此情谁诉。”——《摸鱼儿·更能消几番风雨》

​