🏆 作者简介，愚公搬代码
🏆《头衔》：华为云特约编辑，华为云云享专家，华为开发者专家，华为产品云测专家，CSDN博客专家，阿里云专家博主，腾讯云优秀博主，掘金优秀博主，51CTO博客专家等。
🏆《近期荣誉》：2022年CSDN博客之星TOP2，2022年华为云十佳博主等。
🏆《博客内容》：.NET、Java、Python、Go、Node、前端、IOS、Android、鸿蒙、Linux、物联网、网络安全、大数据、人工智能、U3D游戏、小程序等相关领域知识。
🏆🎉欢迎 👍点赞✍评论⭐收藏

🚀前言

在编程语言中，查找算法是指在一个数据集合中查找某个元素是否存在的算法。常见的查找算法包括：

1. 顺序查找（Sequential Search）：逐个遍历数据集来查找目标元素，时间复杂度为O(n)。

2. 二分查找（Binary Search）：在有序数据集合中，从中间位置作为起点不断划分区间并查找，时间复杂度为O(log n)。

3. 插值查找（Interpolation Search）：在有序数据集合中，根据目标元素与数据集合首尾之间的差值，利用插值估算目标元素的位置，时间复杂度为O(log log n)或O(n)。

4. 斐波那契查找（Fibonacci Search）：在有序数据集合中，根据斐波那契数列调整中间点的位置来查找，时间复杂度为O(log n)。

5. B树查找（B-Tree Search）：在平衡的B树中查找元素，时间复杂度为O(log n)。

6. 哈希查找（Hash Search）：通过哈希函数将元素映射到哈希表中，并在哈希表中查找元素，时间复杂度为O(1)。

7. 分块查找（Block Search）：将数据集合划分为若干块，在每个块中进行二分查找或顺序查找，时间复杂度为O(sqrt(n))。

以上算法都有各自适用的场景，开发者需要根据数据集合的特性和需求选择最适合的算法来进行查找。

🚀一、二叉树查找

🔎1.基本思想

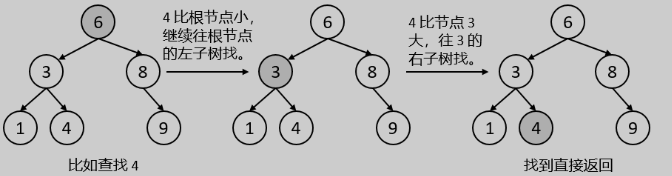
二叉树查找算法基于二叉树的特性，即每个节点最多有两个子节点，且左子节点的值小于父节点的值，右子节点的值大于父节点的值。基本思想如下：

1. 从根节点开始，将要查找的值与当前节点的值进行比较。
2. 如果要查找的值等于当前节点的值，则查找成功。
3. 如果要查找的值小于当前节点的值，则在左子树中继续查找。
4. 如果要查找的值大于当前节点的值，则在右子树中继续查找。
5. 如果左子树或右子树为空，则查找失败。

具体实现可以使用递归或迭代的方式进行。在递归实现中，每次递归调用时传入当前节点作为参数，继续比较子节点的值，直到找到要查找的节点或子树为空为止。在迭代实现中，使用一个指针从根节点开始遍历，比较每个节点的值，直到找到要查找的节点或遍历完整个树为止。

🔎2.复杂度分析

二叉树查找算法的复杂度分析取决于二叉树的结构和被查找的元素所在的位置。假设二叉树的节点个数为n，则二叉树的高度不超过log(n)，因此对于一棵平衡二叉树而言，时间复杂度为O(log(n))，是一种较高效的查找算法。

在最坏情况下，如果二叉树退化为一条链表，则查找的时间复杂度为O(n)，这种情况下算法效率比较低。因此，在实际应用中，需要选择合适的二叉树结构来保证算法的高效性。

🔎3.应用场景

二叉树查找算法常用于数据的存储和查找。以下是一些应用场景：

1. 字典查找：使用二叉查找树可以快速地查找到某个单词是否在字典中存在。

2. 数据库索引：数据库中的索引和二叉查找树的结构非常相似，可以用二叉查找树来实现数据库的索引功能。

3. 文件系统：文件系统中的目录树可以被看作是一种二叉查找树结构，可以使用二叉查找树来实现文件的查找、删除和修改等操作。

4. 路由表：网络路由表中的路由器也可以被看作是一种二叉查找树结构，可以使用二叉查找树来实现路由表的查询。

5. 游戏AI：在游戏中，可以使用二叉查找树来实现AI的行为决策，例如确定目标、寻找路径等。

🔎4.示例

public class BSTNode {
 
    public int Key { get; set; }
 
    public int Index { get; set; }
 
    public BSTNode Left { get; set; }
 
    public BSTNode Right { get; set; }
 
    public BSTNode(int key, int index) {
        Key = key;
        Index = index;
    }
 
    public void Insert(int key, int index) {
        var tree = new BSTNode(key, index);
        if (tree.Key <= Key) {
            if (Left == null) {
                Left = tree;
            }
            else {
                Left.Insert(key, index);
            }
        }
        else {
            if (Right == null) {
                Right = tree;
            }
            else {
                Right.Insert(key, index);
            }
        }
    }
 
    public int Search(int key) {
        //找左子节点
        var left = Left?.Search(key);
        if (left.HasValue && left.Value != -1) return left.Value;
        //找当前节点
        if (Key == key) return Index;
        //找右子节点
        var right = Right?.Search(key);
        if (right.HasValue && right.Value != -1) return right.Value;
        //找不到时返回-1
        return -1;
    }
 
}

int[] array = { 43, 69, 11, 72, 28, 21, 56, 80, 48, 94, 32, 8 };

Console.WriteLine(BinaryTreeSearch(array));

Console.ReadKey();

static int BinaryTreeSearch(int[] array)
{
    var bstNode = new BSTNode(array[0], 0);
    for (int i = 1; i < array.Length; i++)
    {
        bstNode.Insert(array[i], i);
    }
    return bstNode.Search(80);
}

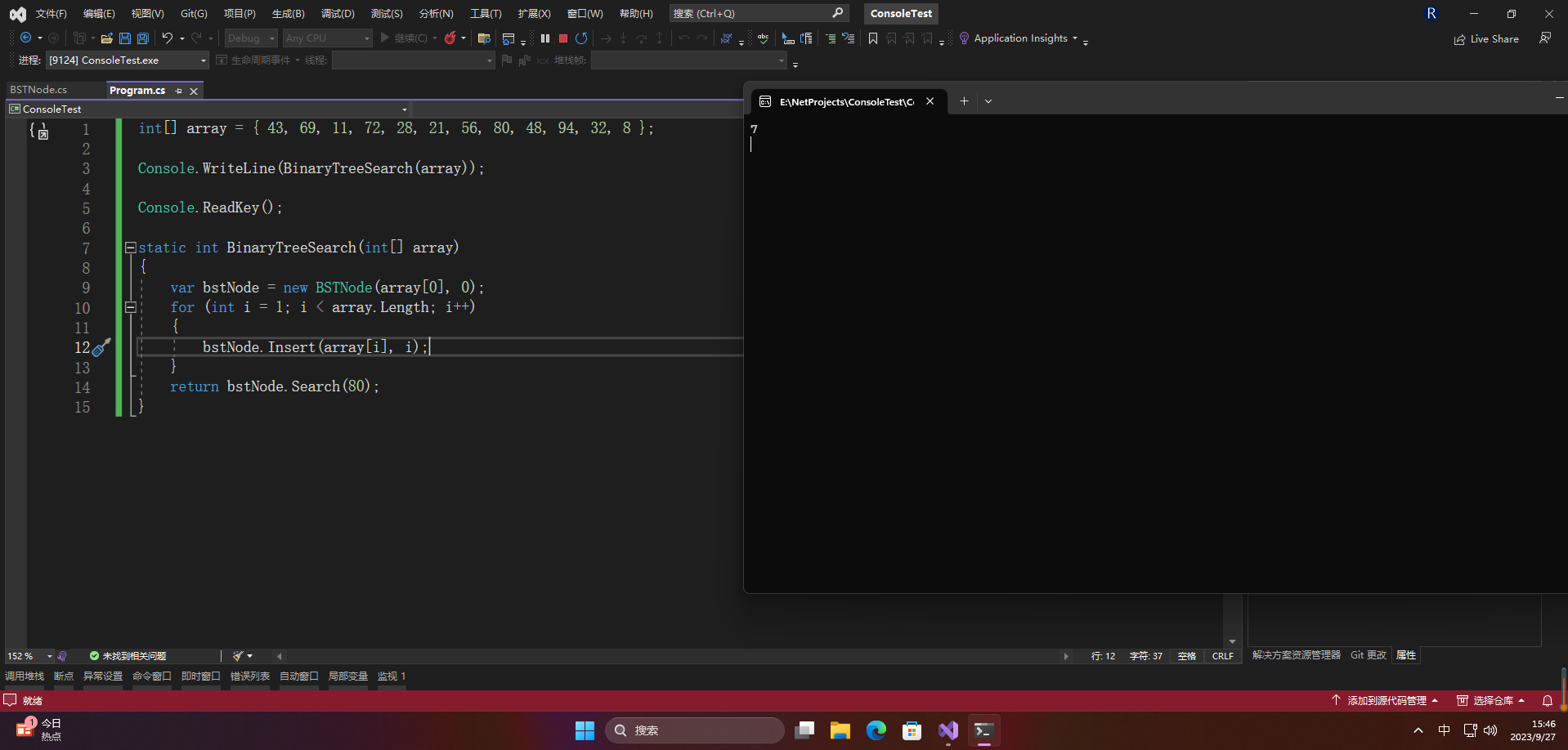
在最坏的情况下二叉树查找的时间复杂度为：O(n) ，在平均情况下的时间复杂度为： O(logn) 。

🚀二、2-3树

🔎1.基本思想

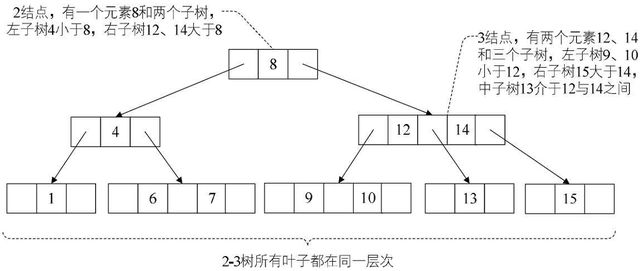
2-3树是一种自平衡查找树，它的基本思想是将数据存储在树节点中，每个节点可以包含一个或两个关键字，同时可能有一到两个子节点。在2-3树中，每个节点最多可以包含3个指针（子节点或数据项），因此，二叉树中的每个节点都有两个或三个儿子。

2-3树的节点有两种类型：2节点和3节点。2节点包含一个关键字和两个子节点，3节点包含两个关键字和三个子节点。2节点上如果插入一个元素，则该节点变成一个3节点，3节点上如果插入一个元素，则该节点会分裂成两个2节点。

2-3树的基本操作包括：插入、查找和删除。插入过程会保持树的平衡性，保证每个节点都是2节点或3节点。查找过程与二叉查找树类似，但是由于2-3树的平衡性，查找效率更高。删除操作需要考虑多种情况，包括删除的元素在2节点或3节点中、删除元素后导致子树不平衡等等。删除过程会保持2-3树的平衡性。

2-3树的基本思想是将数据存储在树节点中，通过维护2节点和3节点的性质来保持树的平衡性，实现高效的查找、插入和删除操作。

🔎2.复杂度分析

2-3树是一种自平衡的树，能够保证树的高度始终为O(log n)，使得插入、查找和删除的复杂度都是O(log n)的时间复杂度。

具体来说，插入操作需要进行以下步骤：

1. 在树中找到要插入的位置。

2. 在叶子节点上进行插入操作。

3. 如果插入导致一个节点包含3个关键字，则进行分裂操作，即将该节点分成两个节点，并将中间的关键字提升到父节点中。

由于每次插入操作都会使得树的高度最多增加1，因此插入操作的时间复杂度为O(log n)。

查找操作也与普通树一样，根据关键字的大小递归查找，时间复杂度为O(log n)。

删除操作需要进行以下步骤：

1. 找到要删除的节点。

2. 如果要删除的节点是一个叶子节点，则直接删除。

3. 如果要删除的节点是一个内部节点，则通过一些操作将其转化为一个叶子节点，然后再删除。

由于删除节点可能会导致节点关键字个数不足，需要进行一些调整操作，使得树能够继续保持2-3树的性质，因此删除操作的时间复杂度也为O(log n)。

🔎3.应用场景

2-3树是一种自平衡二叉查找树，它的应用场景包括：

1. 数据库中的索引结构：2-3树可以用于数据库中的索引结构，因为它可以快速地进行插入、删除和查找操作。

2. 编译器中的符号表：编译器中符号表用于存储程序中的标识符，如变量名、函数名等。2-3树可以用来实现符号表，以便快速查找标识符。

3. 操作系统中的文件系统：文件系统需要维护大量的文件和目录信息。2-3树可以用来实现文件系统中的文件结构和目录结构，以便快速查找和访问文件和目录。

4. 网络路由表：网络路由表用于存储路由信息，2-3树可以用来实现网络路由表，以便快速查找和转发数据包。

5. 程序设计中的排序算法：2-3树可以用来实现排序算法，如2-3树排序算法和归并排序算法，以便快速地对数据进行排序。

2-3树广泛应用于数据结构、算法、编译器、操作系统和网络等领域。

🔎4.示例

2-3查找树（2-3 Tree）是一种自平衡的二叉查找树，用于实现有序数据的存储和检索。它的特点是每个节点可以包含1个或2个键，并且有两种类型的节点：2-节点和3-节点。以下是C#中实现2-3查找树的基本算法和使用示例。

首先，创建一个2-3查找树的节点类：

public class Node
{
    public int[] Keys { get; private set; }
    public Node[] Children { get; private set; }

    public Node()
    {
        Keys = new int[2];
        Children = new Node[3];
    }
}

然后，创建2-3查找树的主要类：

public class TwoThreeTree
{
    private Node root;

    public TwoThreeTree()
    {
        root = null;
    }

    public void Insert(int key)
    {
        root = Insert(root, key);
    }

    private Node Insert(Node node, int key)
    {
        if (node == null)
        {
            node = new Node();
            node.Keys[0] = key;
        }
        else if (node.Keys[1] == 0)
        {
            if (key < node.Keys[0])
            {
                node.Keys[1] = node.Keys[0];
                node.Keys[0] = key;
            }
            else
            {
                node.Keys[1] = key;
            }
        }
        else if (key < node.Keys[0])
        {
            node.Children[0] = Insert(node.Children[0], key);
        }
        else if (key > node.Keys[1])
        {
            node.Children[2] = Insert(node.Children[2], key);
        }
        else
        {
            node.Children[1] = Insert(node.Children[1], key);
        }

        return node;
    }

    public bool Search(int key)
    {
        return Search(root, key);
    }

    private bool Search(Node node, int key)
    {
        if (node == null)
        {
            return false;
        }

        if (node.Keys[0] == key || node.Keys[1] == key)
        {
            return true;
        }
        else if (key < node.Keys[0])
        {
            return Search(node.Children[0], key);
        }
        else if (key > node.Keys[1] || (node.Keys[1] == 0))
        {
            return Search(node.Children[2], key);
        }
        else
        {
            return Search(node.Children[1], key);
        }
    }
}

这是一个简化的2-3查找树实现示例。你可以根据需要添加更多功能，如删除节点、遍历树等。

下面是使用示例：

class Program
{
    static void Main(string[] args)
    {
        TwoThreeTree tree = new TwoThreeTree();

        tree.Insert(10);
        tree.Insert(5);
        tree.Insert(15);

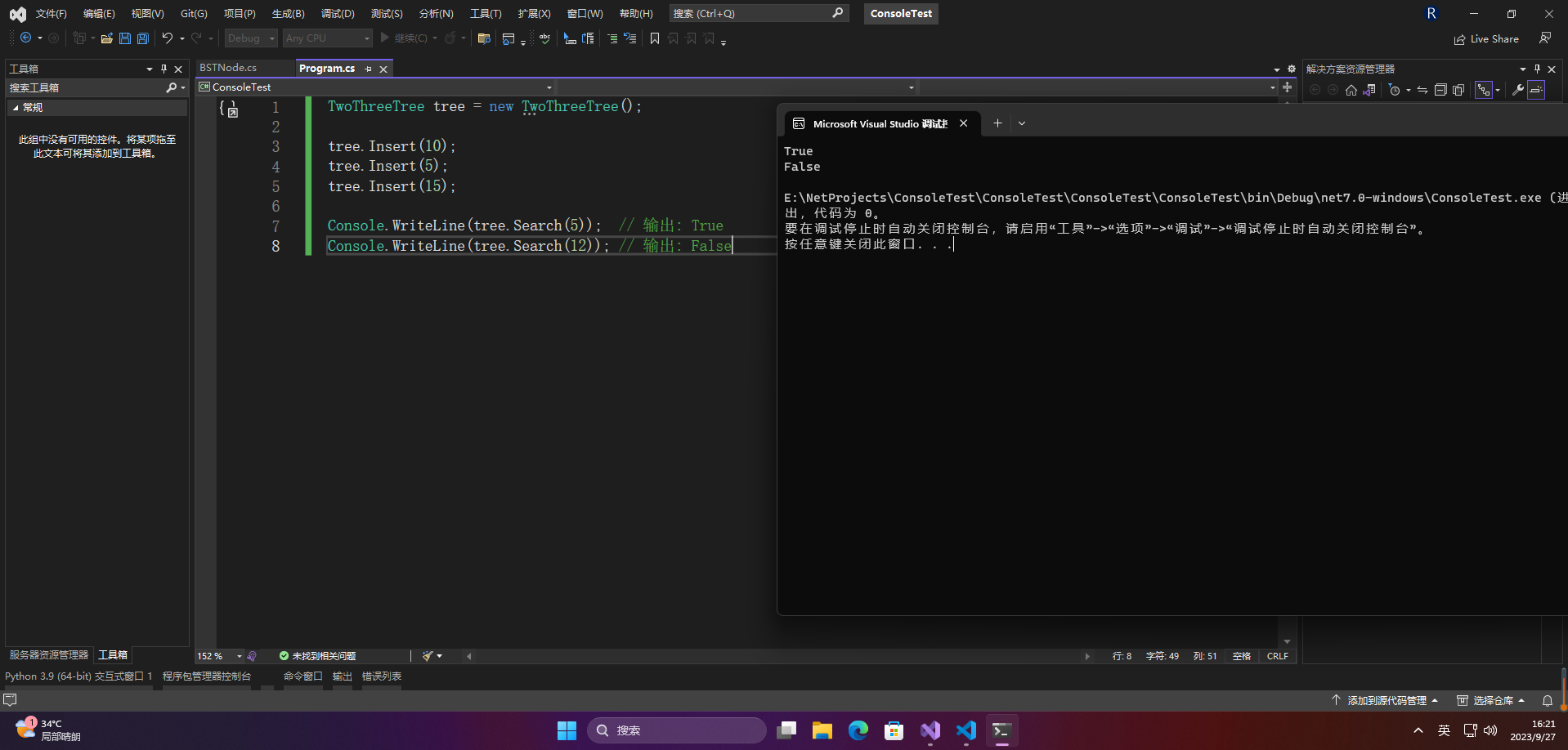
        Console.WriteLine(tree.Search(5));  // 输出: True
        Console.WriteLine(tree.Search(12)); // 输出: False
    }
}

🚀三、红黑树

红黑树具体介绍可以看：https://www.bilibili.com/read/cv17486236/

🔎1.基本思想

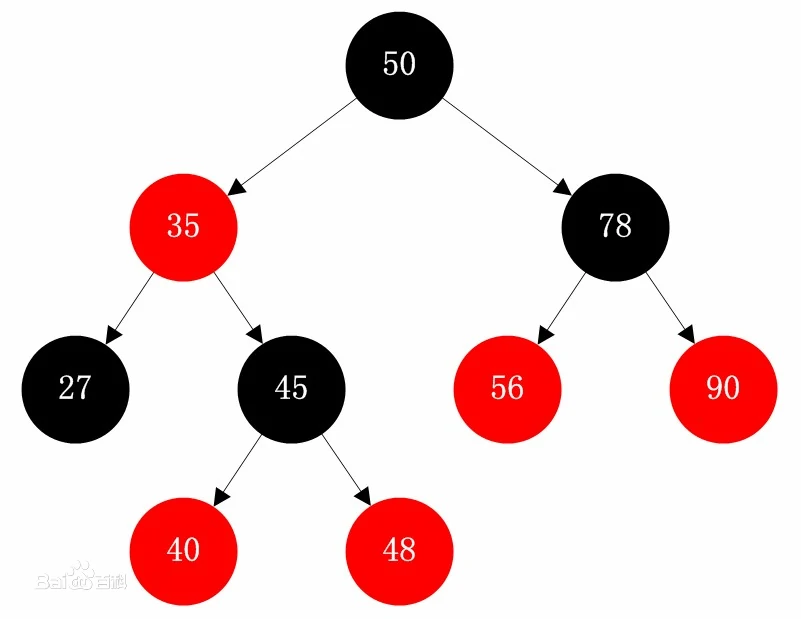
红黑树是一种自平衡二叉搜索树，它的基本思想是通过对树节点的颜色进行限制和变换，来保证在树的基本结构上能够保持平衡性，从而实现高效的查找、插入和删除操作。

具体来说，红黑树中的每个节点都会被标记为红色或黑色，同时满足以下条件：

1. 根节点为黑色；
2. 所有叶子节点（NULL节点）为黑色；
3. 如果一个节点为红色，则它的两个子节点都必须是黑色；
4. 从任意节点到其每个叶子节点的所有路径都必须包含相同数量的黑色节点；

这些限制保证了树的高度不会超过2log(N+1)，其中N为树中节点的数量，因此红黑树的查找、插入和删除操作都可以在O(logN)的时间复杂度内完成。

🔎2.复杂度分析

红黑树的插入、查找和删除操作的时间复杂度均为O(log n)，其中n为红黑树中节点的数量。

这是由红黑树的平衡性质所决定的。红黑树的每个节点都被标记为红色或黑色，并且满足以下约束条件：

1. 根节点是黑色的。
2. 每个叶子节点都是黑色的。
3. 如果一个节点是红色的，则它的子节点必须是黑色的。
4. 从任意一个节点到其每个叶子节点的所有路径都包含相同数量的黑色节点。

这些约束条件确保了红黑树的高度不会超过log n，从而使得插入、查找和删除操作的时间复杂度都能够保持在O(log n)。

需要注意的是，在红黑树中进行查找、插入和删除操作时需要注意平衡性质的维护，因此实现红黑树算法的实际时间复杂度可能会略微高于O(log n)。

🔎3.应用场景

红黑树算法广泛应用于实现一些高效的数据结构，例如：

1. C++ STL中的set、map以及multiset、multimap等，这些数据结构底层都是基于红黑树实现的；

2. Java中的TreeMap和TreeSet，也是基于红黑树实现的；

3. Linux内核中的进程调度，以及各种内核数据结构（例如文件系统、网络协议栈等），也是使用红黑树来进行处理的；

4. 数据库系统中的索引（例如B+树、B树等），也使用了红黑树算法来进行内部结构的优化；

5. 操作系统中的文件系统（例如EXT2、EXT3等）中，使用了红黑树来维护文件的目录结构。

红黑树算法是一种非常高效、稳定的数据结构，可以在各种场合下发挥其优越的性能和稳定性。

🔎4.示例

当然可以帮助您实现一个红黑树算法并提供一些示例用法。红黑树是一种自平衡的二叉搜索树，通常用于实现字典等数据结构，以确保插入、删除和查找操作的平均时间复杂度为O(log n)。

以下是一个简单的C#实现示例：

using System;

public enum NodeColor
{
    Red,
    Black
}

public class RedBlackNode<T> where T : IComparable<T>
{
    public T Data { get; set; }
    public RedBlackNode<T> Parent { get; set; }
    public RedBlackNode<T> Left { get; set; }
    public RedBlackNode<T> Right { get; set; }
    public NodeColor Color { get; set; }
}

public class RedBlackTree<T> where T : IComparable<T>
{
    private RedBlackNode<T> root;

    public void Insert(T value)
    {
        var newNode = new RedBlackNode<T> { Data = value, Color = NodeColor.Red };

        if (root == null)
        {
            root = newNode;
        }
        else
        {
            var currentNode = root;
            while (currentNode != null)
            {
                int compareResult = value.CompareTo(currentNode.Data);
                if (compareResult < 0)
                {
                    if (currentNode.Left == null)
                    {
                        currentNode.Left = newNode;
                        newNode.Parent = currentNode;
                        break;
                    }
                    currentNode = currentNode.Left;
                }
                else
                {
                    if (currentNode.Right == null)
                    {
                        currentNode.Right = newNode;
                        newNode.Parent = currentNode;
                        break;
                    }
                    currentNode = currentNode.Right;
                }
            }
        }

        InsertFixup(newNode);
    }

    // 插入修复函数，确保红黑树的性质得以维护
    private void InsertFixup(RedBlackNode<T> node)
    {
        while (node.Parent != null && node.Parent.Color == NodeColor.Red)
        {
            if (node.Parent == node.Parent.Parent.Left)
            {
                var uncle = node.Parent.Parent.Right;
                if (uncle != null && uncle.Color == NodeColor.Red)
                {
                    node.Parent.Color = NodeColor.Black;
                    uncle.Color = NodeColor.Black;
                    node.Parent.Parent.Color = NodeColor.Red;
                    node = node.Parent.Parent;
                }
                else
                {
                    if (node == node.Parent.Right)
                    {
                        node = node.Parent;
                        RotateLeft(node);
                    }
                    node.Parent.Color = NodeColor.Black;
                    node.Parent.Parent.Color = NodeColor.Red;
                    RotateRight(node.Parent.Parent);
                }
            }
            else
            {
                var uncle = node.Parent.Parent.Left;
                if (uncle != null && uncle.Color == NodeColor.Red)
                {
                    node.Parent.Color = NodeColor.Black;
                    uncle.Color = NodeColor.Black;
                    node.Parent.Parent.Color = NodeColor.Red;
                    node = node.Parent.Parent;
                }
                else
                {
                    if (node == node.Parent.Left)
                    {
                        node = node.Parent;
                        RotateRight(node);
                    }
                    node.Parent.Color = NodeColor.Black;
                    node.Parent.Parent.Color = NodeColor.Red;
                    RotateLeft(node.Parent.Parent);
                }
            }
        }
        root.Color = NodeColor.Black;
    }

    // 左旋操作
    private void RotateLeft(RedBlackNode<T> node)
    {
        var rightChild = node.Right;
        node.Right = rightChild.Left;
        if (rightChild.Left != null)
        {
            rightChild.Left.Parent = node;
        }
        rightChild.Parent = node.Parent;
        if (node.Parent == null)
        {
            root = rightChild;
        }
        else if (node == node.Parent.Left)
        {
            node.Parent.Left = rightChild;
        }
        else
        {
            node.Parent.Right = rightChild;
        }
        rightChild.Left = node;
        node.Parent = rightChild;
    }

    // 右旋操作
    private void RotateRight(RedBlackNode<T> node)
    {
        var leftChild = node.Left;
        node.Left = leftChild.Right;
        if (leftChild.Right != null)
        {
            leftChild.Right.Parent = node;
        }
        leftChild.Parent = node.Parent;
        if (node.Parent == null)
        {
            root = leftChild;
        }
        else if (node == node.Parent.Left)
        {
            node.Parent.Left = leftChild;
        }
        else
        {
            node.Parent.Right = leftChild;
        }
        leftChild.Right = node;
        node.Parent = leftChild;
    }

    // 其他操作，如删除和查找，也可以在此实现
}

// 使用示例
public class Program
{
    public static void Main(string[] args)
    {
        RedBlackTree<int> tree = new RedBlackTree<int>();
        tree.Insert(10);
        tree.Insert(20);
        tree.Insert(5);
        tree.Insert(30);
        tree.Insert(15);

        // 此处可以进行其他操作，如查找、删除等

        Console.WriteLine("红黑树的根节点值: " + tree.Root.Data);
    }
}

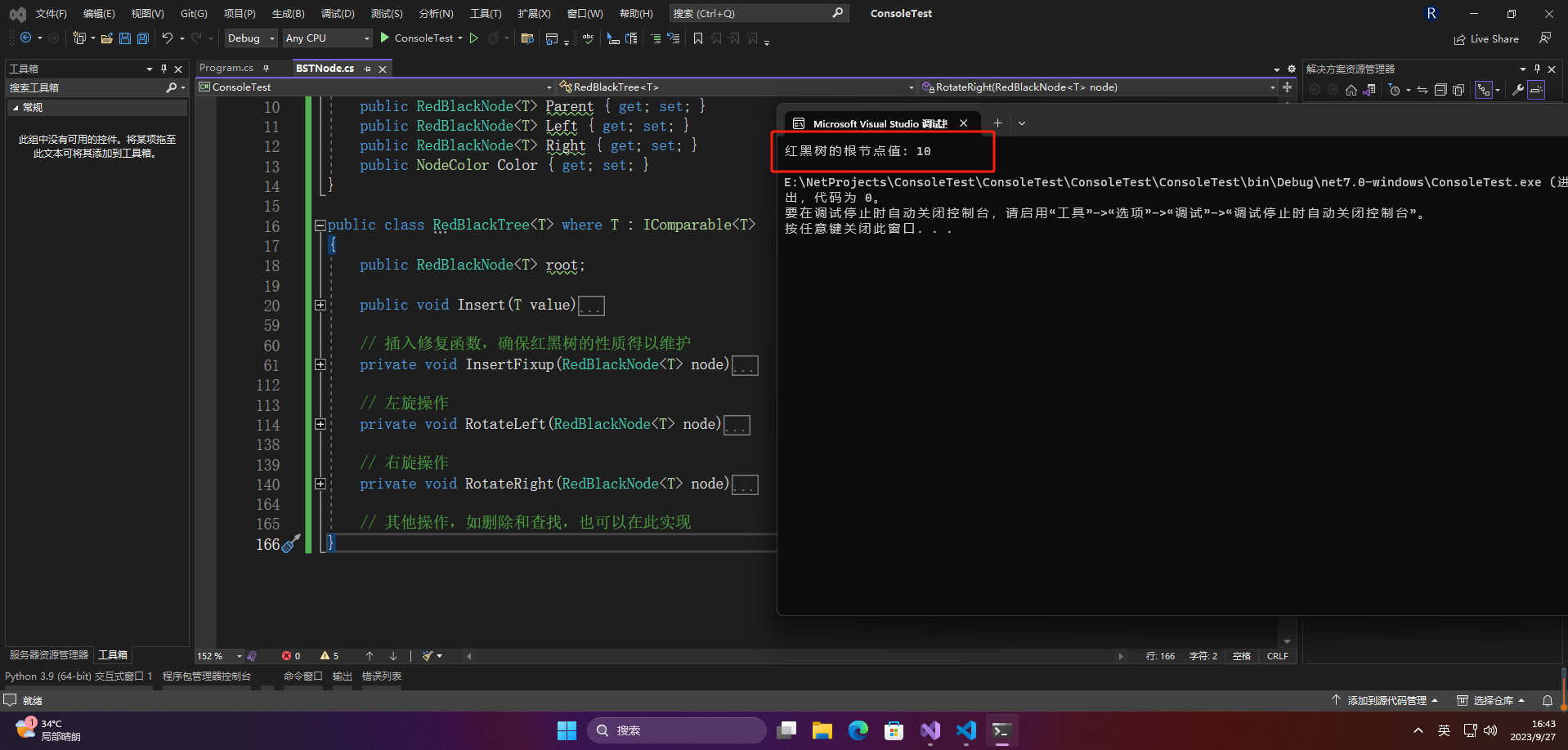
这是一个基本的红黑树实现，包括插入操作和相关的修复函数。您可以根据自己的需求扩展这个实现，并添加其他操作如查找和删除。

🚀四、B树和B+树

🔎1.基本思想

B树和B+树都是一种多路搜索树，用于在磁盘等外部存储设备上实现高效的数据存储和检索。它们的基本思想是将数据按照一定的规则分组并组织成一棵多叉树，在每个节点上存储一定数量的关键字和指向子节点的指针，以实现快速的查找、插入和删除操作。

B树的基本思想是保证每个节点至少填满一半的关键字，以达到较好的性能。其优点是对于大规模数据的插入和删除操作，它仍然能够保持较好的性能，但缺点是每个节点都需要存储一定数量的指针，导致存储空间的浪费。

B+树在B树的基础上进行了改进，将所有的关键字都存储在叶子节点中，非叶子节点只存储关键字和指向子节点的指针。这种设计能够大大减少存储空间的浪费，并且能够通过叶子节点间的链表快速定位到某个范围内的数据。B+树在磁盘等外部存储设备上的表现比B树更优，因此被广泛应用于数据库和文件系统中。

🔎2.复杂度分析

B树和B+树的复杂度分析主要针对它们的查找、插入和删除操作。

1. 查找

B树和B+树的查找操作都是从根节点开始，按照树中节点的关键字大小，逐层向下查找，直到找到对应的叶子节点或者未找到。

在B树中，由于每个节点中包含了多个关键字和子节点指针，因此它的查找复杂度为O(h)，其中h为树的高度。

在B+树中，非叶子节点只包含子节点的指针，而所有数据都存储在叶子节点中，因此它的查找复杂度也为O(h)。

2. 插入

B树和B+树的插入操作都是从根节点开始，按照树中节点的关键字大小，逐层向下查找，找到对应的叶子节点后进行插入。

在B树中，如果插入导致节点关键字数量超过了最大值，则需要进行节点的分裂操作。分裂操作的复杂度为O(n)，其中n为节点关键字数量。

在B+树中，插入操作只影响到叶子节点，因此不需要进行节点的分裂操作。它的插入复杂度为O(logn)。

3. 删除

B树和B+树的删除操作也都是从根节点开始，按照树中节点的关键字大小，逐层向下查找，找到对应的叶子节点后进行删除。

在B树中，如果删除导致节点关键字数量低于最小值，则需要进行节点的合并操作。合并操作的复杂度也为O(n)。

在B+树中，由于所有数据都存储在叶子节点中，因此删除操作只需要将对应的数据从叶子节点中删除即可。它的删除复杂度为O(logn)。

总体来说，B+树相比于B树在插入和删除操作上具有更优的时间复杂度。在实际应用中，B+树通常被用于数据库等需要频繁进行查找、插入和删除操作的场景中。

🔎3.应用场景

B树和B+树算法适用于一些需要高效处理大量数据的场景，比如数据库系统、文件系统、操作系统内存管理等。

具体而言：

1. 数据库系统：B树和B+树是数据库系统中用于实现索引的常见数据结构。B树可以直接用于数据存储，而B+树则可以更好地支持范围查询和排序操作。

2. 文件系统：B树和B+树可以用来实现文件系统中的目录结构，以支持对文件的快速访问。

3. 操作系统内存管理：操作系统内存管理需要高效地管理大量的内存块，因此可以使用B树和B+树来实现内存地址的管理和分配。

B树和B+树算法的应用场景都是需要高效处理大量数据的场景，可以提高数据的检索、插入、删除等操作的效率。

🔎4.示例

🦋4.1 B树

要实现完整的B树算法，并且提供具体的使用示例，需要考虑各种操作，包括插入、查找、删除等。以下是一个C#示例，演示如何实现B树并进行基本的插入和查找操作。

using System;
using System.Collections.Generic;

public class BTreeNode<T> where T : IComparable<T>
{
    public List<T> Keys { get; set; }
    public List<BTreeNode<T>> Children { get; set; }
    public bool IsLeaf { get; set; }

    public BTreeNode()
    {
        Keys = new List<T>();
        Children = new List<BTreeNode<T>>();
        IsLeaf = true;
    }
}

public class BTree<T> where T : IComparable<T>
{
    private BTreeNode<T> root;
    private int degree;

    public BTree(int degree)
    {
        this.degree = degree;
        root = new BTreeNode<T>();
    }

    public void Insert(T key)
    {
        var rootNode = root;
        if (rootNode.Keys.Count == (2 * degree) - 1)
        {
            var newRoot = new BTreeNode<T> { IsLeaf = false };
            newRoot.Children.Add(rootNode);
            SplitChild(newRoot, 0);
            root = newRoot;
            InsertNonFull(root, key);
        }
        else
        {
            InsertNonFull(rootNode, key);
        }
    }

    public bool Search(T key)
    {
        return SearchNode(root, key) != null;
    }

    private BTreeNode<T> SearchNode(BTreeNode<T> node, T key)
    {
        int i = 0;
        while (i < node.Keys.Count && key.CompareTo(node.Keys[i]) > 0)
        {
            i++;
        }

        if (i < node.Keys.Count && key.CompareTo(node.Keys[i]) == 0)
        {
            return node;
        }

        if (node.IsLeaf)
        {
            return null;
        }

        return SearchNode(node.Children[i], key);
    }

    private void InsertNonFull(BTreeNode<T> node, T key)
    {
        int index = node.Keys.Count - 1;

        if (node.IsLeaf)
        {
            node.Keys.Add(default(T));

            while (index >= 0 && key.CompareTo(node.Keys[index]) < 0)
            {
                node.Keys[index + 1] = node.Keys[index];
                index--;
            }

            node.Keys[index + 1] = key;
        }
        else
        {
            while (index >= 0 && key.CompareTo(node.Keys[index]) < 0)
            {
                index--;
            }

            index++;

            if (node.Children[index].Keys.Count == (2 * degree) - 1)
            {
                SplitChild(node, index);

                if (key.CompareTo(node.Keys[index]) > 0)
                {
                    index++;
                }
            }

            InsertNonFull(node.Children[index], key);
        }
    }

    private void SplitChild(BTreeNode<T> parentNode, int childIndex)
    {
        var childNode = parentNode.Children[childIndex];
        var newNode = new BTreeNode<T> { IsLeaf = childNode.IsLeaf };
        parentNode.Keys.Insert(childIndex, childNode.Keys[degree - 1]);
        parentNode.Children.Insert(childIndex + 1, newNode);

        newNode.Keys.AddRange(childNode.Keys.GetRange(degree, degree - 1));
        childNode.Keys.RemoveRange(degree - 1, degree);

        if (!childNode.IsLeaf)
        {
            newNode.Children.AddRange(childNode.Children.GetRange(degree, degree));
            childNode.Children.RemoveRange(degree, degree);
        }
    }
}

现在，让我们看一下如何使用这个B树类：

class Program
{
    static void Main()
    {
        BTree<int> bTree = new BTree<int>(3); // 创建一个B树，度为3

        // 插入一些键值对
        bTree.Insert(10);
        bTree.Insert(20);
        bTree.Insert(5);
        bTree.Insert(15);

        // 查找键
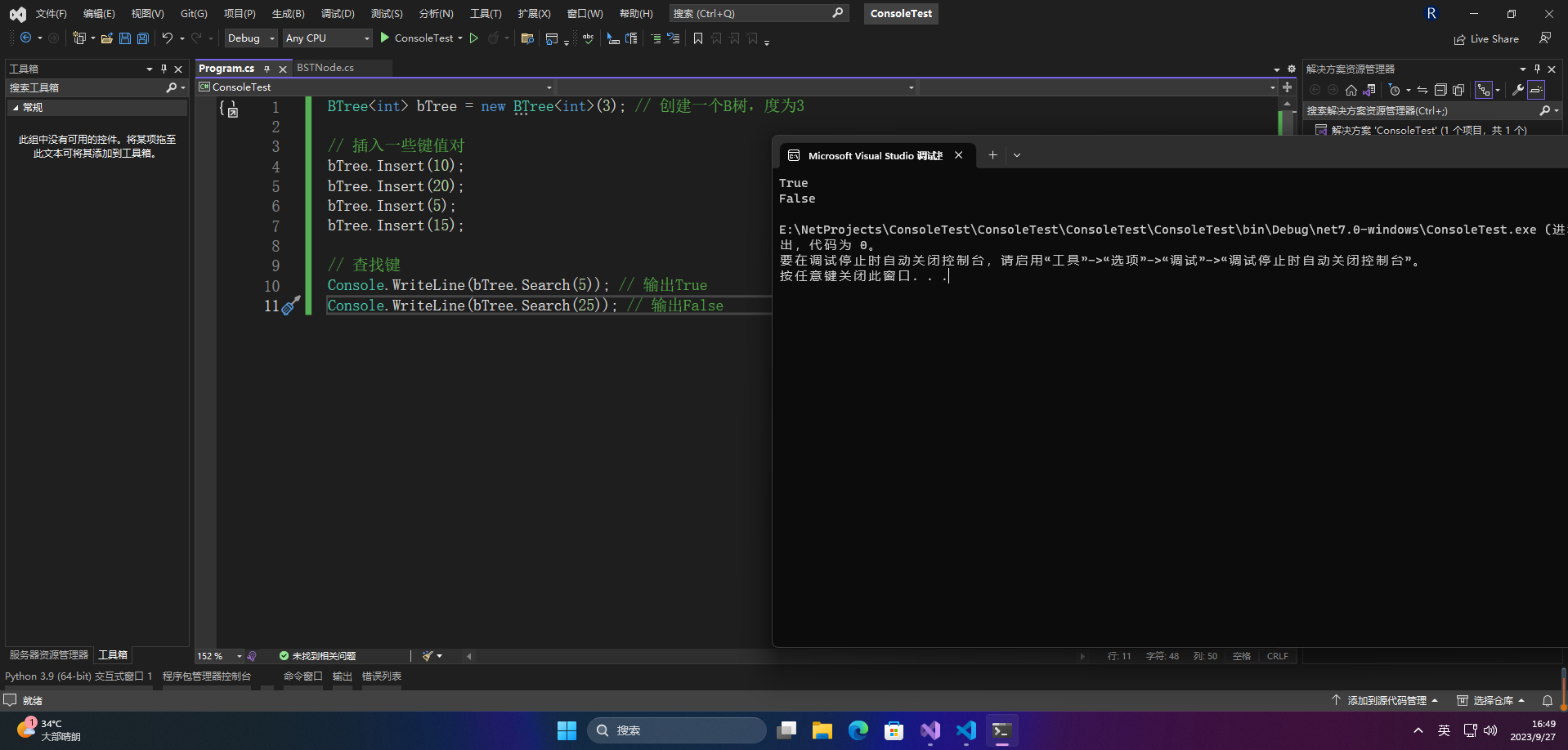
        Console.WriteLine(bTree.Search(5)); // 输出True
        Console.WriteLine(bTree.Search(25)); // 输出False
    }
}

🦋4.2 B+树

实现完整的B+树算法并提供具体使用示例需要相当多的代码和详细的讲解。

首先，让我们创建B+树的节点类和B+树类：

using System;
using System.Collections.Generic;

public class BPlusTreeNode<TKey, TValue> where TKey : IComparable<TKey>
{
    public List<TKey> Keys { get; set; }
    public List<TValue> Values { get; set; }
    public List<BPlusTreeNode<TKey, TValue>> Children { get; set; }
    public BPlusTreeNode<TKey, TValue> Next { get; set; } // 指向下一个叶子节点
    public bool IsLeaf { get; set; }
    public TValue Value { get; set; }

    public BPlusTreeNode()
    {
        Keys = new List<TKey>();
        Values = new List<TValue>();
        Children = new List<BPlusTreeNode<TKey, TValue>>();
        IsLeaf = true;
    }
}

public class BPlusTree<TKey, TValue> where TKey : IComparable<TKey>
{
    private BPlusTreeNode<TKey, TValue> root;
    private int degree;

    public BPlusTree(int degree)
    {
        this.degree = degree;
        root = new BPlusTreeNode<TKey, TValue> { IsLeaf = true };
    }

    public void Insert(TKey key, TValue value)
    {
        if (root.Keys.Count == (2 * degree) - 1)
        {
            var newRoot = new BPlusTreeNode<TKey, TValue> { IsLeaf = false };
            newRoot.Children.Add(root);
            SplitChild(newRoot, 0);
            root = newRoot;
        }
        InsertNonFull(root, key, value);
    }

    private void InsertNonFull(BPlusTreeNode<TKey, TValue> node, TKey key, TValue value)
    {
        int index = node.Keys.Count - 1;

        if (node.IsLeaf)
        {
            node.Keys.Add(default(TKey));
            node.Values.Add(default(TValue));

            while (index >= 0 && key.CompareTo(node.Keys[index]) < 0)
            {
                node.Keys[index + 1] = node.Keys[index];
                node.Values[index + 1] = node.Values[index];
                index--;
            }

            node.Keys[index + 1] = key;
            node.Values[index + 1] = value;
        }
        else
        {
            while (index >= 0 && key.CompareTo(node.Keys[index]) < 0)
            {
                index--;
            }

            index++;

            if (node.Children[index].Keys.Count == (2 * degree) - 1)
            {
                SplitChild(node, index);

                if (key.CompareTo(node.Keys[index]) > 0)
                {
                    index++;
                }
            }

            InsertNonFull(node.Children[index], key, value);
        }
    }

    public TValue Search(TKey key)
    {
        return SearchNode(root, key);
    }

    private TValue SearchNode(BPlusTreeNode<TKey, TValue> node, TKey key)
    {
        int index = 0;
        while (index < node.Keys.Count && key.CompareTo(node.Keys[index]) >= 0)
        {
            index++;
        }

        if (node.IsLeaf)
        {
            if (index > 0 && key.CompareTo(node.Keys[index - 1]) == 0)
            {
                return node.Values[index - 1];
            }
            else
            {
                return default(TValue);
            }
        }
        else
        {
            return SearchNode(node.Children[index], key);
        }
    }

    private void SplitChild(BPlusTreeNode<TKey, TValue> parentNode, int childIndex)
    {
        var childNode = parentNode.Children[childIndex];
        var newNode = new BPlusTreeNode<TKey, TValue> { IsLeaf = childNode.IsLeaf };
        parentNode.Keys.Insert(childIndex, childNode.Keys[degree - 1]);
        parentNode.Values.Insert(childIndex, childNode.Values[degree - 1]);
        parentNode.Children.Insert(childIndex + 1, newNode);

        newNode.Keys.AddRange(childNode.Keys.GetRange(degree, degree - 1));
        newNode.Values.AddRange(childNode.Values.GetRange(degree, degree - 1));
        childNode.Keys.RemoveRange(degree - 1, degree);
        childNode.Values.RemoveRange(degree - 1, degree);

        if (!childNode.IsLeaf)
        {
            newNode.Children.AddRange(childNode.Children.GetRange(degree, degree));
            childNode.Children.RemoveRange(degree, degree);
        }
    }
}

现在，让我们看一下如何使用这个B+树类：

class Program
{
    static void Main()
    {
        BPlusTree<int, string> bPlusTree = new BPlusTree<int, string>(3); // 创建一个B+树，度为3

        // 插入一些键值对
        bPlusTree.Insert(10, "Value1");
        bPlusTree.Insert(20, "Value2");
        bPlusTree.Insert(5, "Value3");
        bPlusTree.Insert(15, "Value4");

        // 查找键
        Console.WriteLine(bPlusTree.Search(5)); // 输出 "Value3"
        Console.WriteLine(bPlusTree.Search(25)); // 输出 null
    }
}

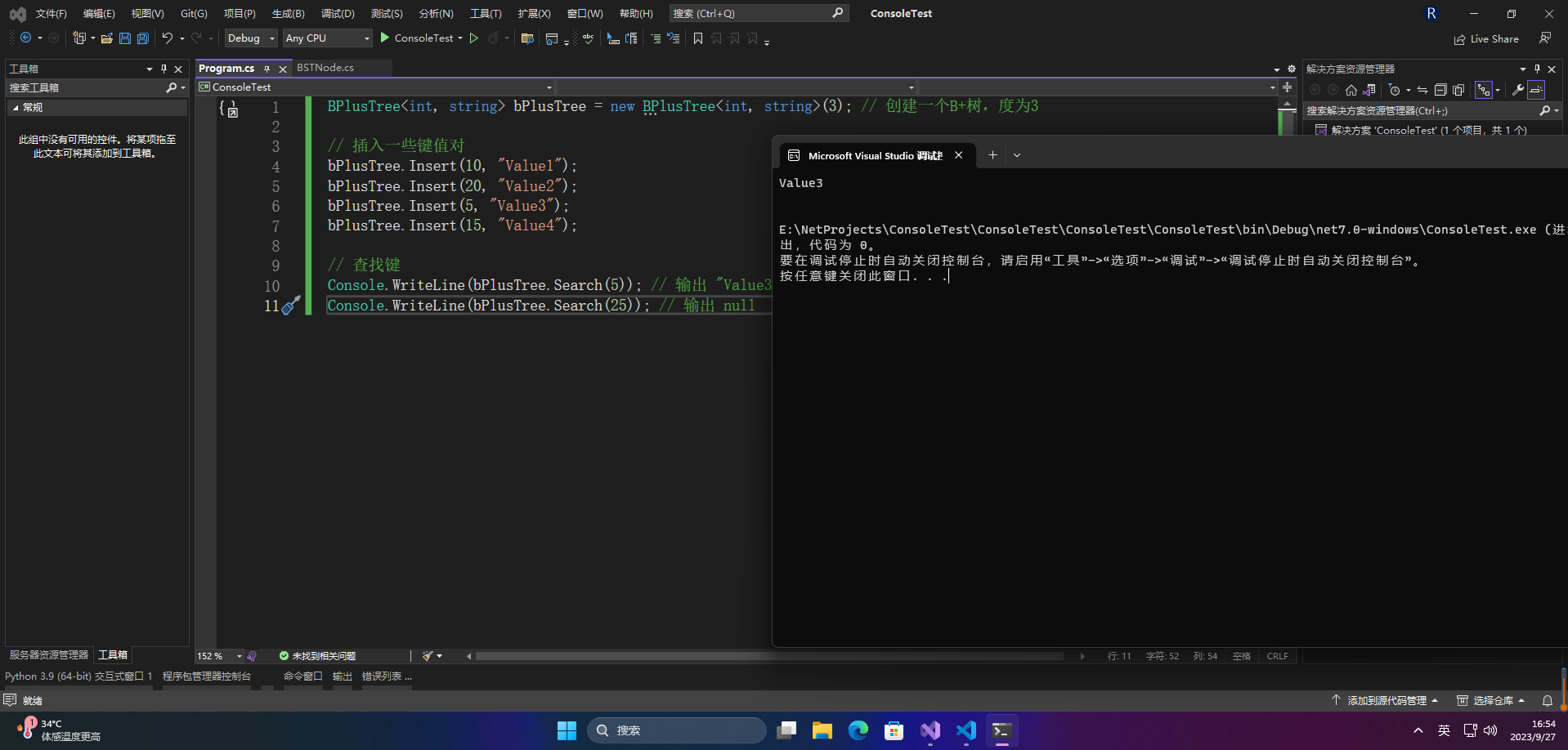
这是一个简单的B+树实现和使用示例。您可以根据需要扩展此实现，并添加删除等操作。希望这个示例对您有所帮助。 B+树的实现通常比这个示例更复杂，因为它需要处理更多的情况和维护索引结构。如果您需要更详细的实现或更复杂的用例，请考虑使用成熟的B+树库或深入学习B+树算法。

🚀感谢：给读者的一封信

亲爱的读者，

我在这篇文章中投入了大量的心血和时间，希望为您提供有价值的内容。这篇文章包含了深入的研究和个人经验，我相信这些信息对您非常有帮助。

如果您觉得这篇文章对您有所帮助，我诚恳地请求您考虑赞赏1元钱的支持。这个金额不会对您的财务状况造成负担，但它会对我继续创作高质量的内容产生积极的影响。

我之所以写这篇文章，是因为我热爱分享有用的知识和见解。您的支持将帮助我继续这个使命，也鼓励我花更多的时间和精力创作更多有价值的内容。

如果您愿意支持我的创作，请扫描下面二维码，您的支持将不胜感激。同时，如果您有任何反馈或建议，也欢迎与我分享。

再次感谢您的阅读和支持！

最诚挚的问候， “愚公搬代码”