【算法】剑指 Offer II 110. 所有路径|797. 所有可能的路径(多语言实现)
【摘要】 剑指 Offer II 110. 所有路径|797. 所有可能的路径:给定一个有 n 个节点的有向无环图,用二维数组 graph 表示,请找到所有从 0 到 n-1 的路径并输出(不要求按顺序)。graph 的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些结点(译者注:有向图是有方向的,即规定了 a→b 你就不能从 b→a ),若为空,就是没有下一个节点了。 样例 1:输...
剑指 Offer II 110. 所有路径|797. 所有可能的路径:
给定一个有 n 个节点的有向无环图,用二维数组 graph 表示,请找到所有从 0 到 n-1 的路径并输出(不要求按顺序)。
graph 的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些结点(译者注:有向图是有方向的,即规定了 a→b 你就不能从 b→a ),若为空,就是没有下一个节点了。
样例 1:
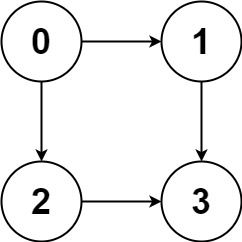
输入:
graph = [[1,2],[3],[3],[]]
输出:
[[0,1,3],[0,2,3]]
解释:
有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
样例 2:
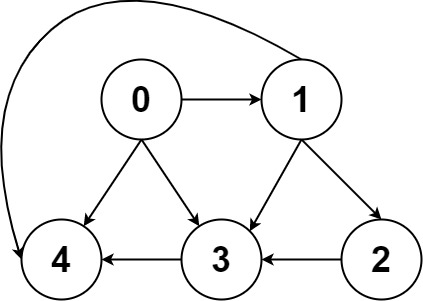
输入:
graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出:
[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
样例 3:
输入:
graph = [[1],[]]
输出:
[[0,1]]
样例 4:
输入:
graph = [[1,2,3],[2],[3],[]]
输出:
[[0,1,2,3],[0,2,3],[0,3]]
样例 5:
输入:
graph = [[1,3],[2],[3],[]]
输出:
[[0,1,2,3],[0,3]]
提示:
- n == graph.length
- 2 <= n <= 15
- 0 <= graph[i][j] < n
- graph[i][j] != i
- 保证输入为有向无环图 (GAD)
分析
- 这道算法题幸好是
无环图,要不然就没那么简单了。 - 遍历路径,找到所有可以到达终点节点的路径就是结果。
- 大部分语言的题解都是用的动态数据结构,所以可以规避一个问题,那就是你要提前知道结果集的最大数量。
- C语言由于是手动去申请内存,所以需要知道结果集的最大数量,当然去申请很大的内存肯定就够放,但是本着算法精神,我们应该申请刚好够用的内存。
- 提示中说
保证输入为有向无环图 (GAD),所以我们可以认为节点间一定有着某种排列的顺序,从头到尾怎样可以有最多的路径呢,那就是在保证没有环路的情况下,所有节点都尽可能多的连接着其他节点。 - 开始节点可以直接到终点节点…途径任何一个节点都能到终点…途径任何二个节点都能到终点…以此类推,所以中间的节点就成了可以任意组合,一共多少种组合,每个节点都是经过或者不经过两种可能,由于头尾的节点是必经经过的,所以最多结果集的数量就是 (n - 2)2 , 也就是
1 << n - 2。
题解
java
class Solution {
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
List<List<Integer>> ans = new ArrayList<>();
Deque<Integer> stack = new ArrayDeque<>();
stack.offerLast(0);
dfs(graph, stack, ans);
return ans;
}
private void dfs(int[][] graph, Deque<Integer> stack, List<List<Integer>> ans) {
if (stack.peekLast() == graph.length - 1) {
ans.add(new ArrayList<>(stack));
return;
}
for (int to : graph[stack.peekLast()]) {
stack.offerLast(to);
dfs(graph, stack, ans);
stack.pollLast();
}
}
}
c
void dfs(int **graph, int *graphColSize, int *returnSize, int **returnColumnSizes, int n, int *stack, int stackSize, int **ans) {
int last = stack[stackSize - 1];
if (last == n) {
int *row = malloc(sizeof(int) * stackSize);
memcpy(row, stack, sizeof(int) * stackSize);
ans[*returnSize] = row;
(*returnColumnSizes)[(*returnSize)++] = stackSize;
return;
}
for (int i = 0; i < graphColSize[last]; ++i) {
int to = graph[last][i];
stack[stackSize] = to;
dfs(graph, graphColSize, returnSize, returnColumnSizes, n, stack, stackSize + 1, ans);
}
}
/**
* Return an array of arrays of size *returnSize.
* The sizes of the arrays are returned as *returnColumnSizes array.
* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
*/
int** allPathsSourceTarget(int** graph, int graphSize, int* graphColSize, int* returnSize, int** returnColumnSizes){
*returnSize = 0;
*returnColumnSizes = malloc(sizeof(int) * (1 << graphSize - 2));
int **ans = malloc(sizeof(int *) * (1 << graphSize - 2));
int *stack = malloc(sizeof(int) * graphSize);
stack[0] = 0;
dfs(graph, graphColSize, returnSize, returnColumnSizes, graphSize - 1, stack, 1, ans);
return ans;
}
c++
class Solution {
private:
void dfs(vector<vector<int>>& graph, vector<int>& stack, vector<vector<int>>& ans) {
if (stack.back() == graph.size() - 1) {
ans.push_back(stack);
return;
}
for (auto& to : graph[stack.back()]) {
stack.push_back(to);
dfs(graph, stack, ans);
stack.pop_back();
}
}
public:
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
vector<vector<int>> ans;
vector<int> stack;
stack.push_back(0);
dfs(graph, stack, ans);
return ans;
}
};
python
class Solution:
def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
ans = list()
stack = list()
def dfs():
last = stack[len(stack) - 1]
if last == len(graph) - 1:
ans.append(stack[:])
return
for to in graph[last]:
stack.append(to)
dfs()
stack.pop()
stack.append(0)
dfs()
return ans
go
func allPathsSourceTarget(graph [][]int) (ans [][]int) {
n := len(graph) - 1
stack := []int{0}
var dfs func()
dfs = func() {
last := stack[len(stack)-1]
if last == n {
ans = append(ans, append([]int{}, stack...))
return
}
for _, to := range graph[last] {
stack = append(stack, to)
dfs()
stack = stack[:len(stack)-1]
}
}
dfs()
return
}
rust
impl Solution {
pub fn all_paths_source_target(graph: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
let mut ans: Vec<Vec<i32>> = Vec::new();
let mut stack: Vec<i32> = Vec::new();
stack.push(0);
Solution::dfs(&graph, graph.len() as i32 - 1, &mut stack, &mut ans);
ans
}
fn dfs(graph: &Vec<Vec<i32>>, n: i32, stack: &mut Vec<i32>, ans: &mut Vec<Vec<i32>>) {
let last = stack[stack.len() - 1];
if last == n {
ans.push(stack.clone());
return;
}
graph[last as usize].iter().for_each(|to| {
stack.push(to.clone());
Solution::dfs(graph, n, stack, ans);
stack.pop();
});
}
}
原题传送门:https://leetcode-cn.com/problems/bP4bmD/
原题传送门:https://leetcode-cn.com/problems/all-paths-from-source-to-target/
非常感谢你阅读本文~
放弃不难,但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子:https://bbs.huaweicloud.cn/community/usersnew/id_1628396583336561 博客原创~
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)