- 微信
- 微博
  
  分享文章到微博
- 复制链接
  
  复制链接到剪贴板

2022CUDA夏季训练营Day2实践

张辉发表于 2022/07/12 14:22:17 2022/07/12

【摘要】 CUDA

前情回顾：

2022CUDA夏季训练营Day1实践 https://bbs.huaweicloud.cn/blogs/364478

CUDA训练营第二天上午介绍了CUDA线程层次的概念，下午介绍了CUDA的矩阵乘法的实现。

上午课件记录：

线程层次的概念：

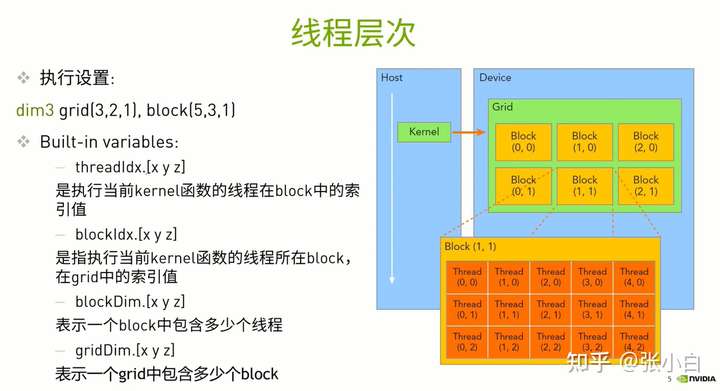
简单说，就是一个grid有多个block,一个block有多个thread.

grid有多大，用gridDim表示它有多少个block，具体分为gridDim.x, gridDim.y，gridDim.z。

block有多大，用blockDim表示它有多少个thread，具体分为blockDim.x，blockDim.y，blockDim.z。

怎么表示thread在block中的相对位置呢？用 threadIdx.x,threadIdx.y,threadIdx.z表示。

怎么表示block在grid中的相对位置呢？用blockIdx.x,blockIdx.y,blockIdx.z表示。

顺便解释下昨天提到的 hello_from_gpu<<<x,y>>>(); 中的x和y是什么意思？它们分别表示 gridDim和blockDim。

对于下面这个函数：

表示gridDim是1，表示grid有1个block，blockDim是4。表示block有4个thread。

所以对于上面的核函数，相当于有4个thread分别执行了 c[n]=a[n]+b[n]的操作，n=threadIdx.x

在调用的时候，所有的CUDA核都是执行同一个函数。这与CPU多线程可能会执行不同的任务不同。

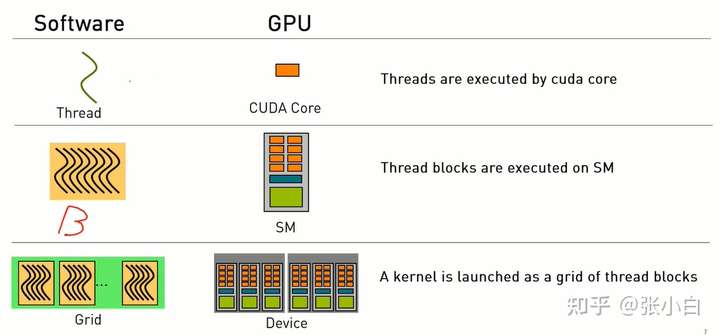
如上图所示，Thread在CUDA core中执行，Block在 SM中执行，Grid在Device中执行。

那么，CUDA是如何执行的呢？看下面这张图：

如果没有block的概念，要同时进行同步、通信、协作时，整体的核心都要产生等待的行为，如要进行扩展时，扩展的越多等待也越多。所以性能会受影响。

但是有block的概念后，可以实现可扩展性。用block或warp就可以很容易实现扩展了。

如何找到线程该处理的数据在哪里呢？这就要提到线程索引的概念。

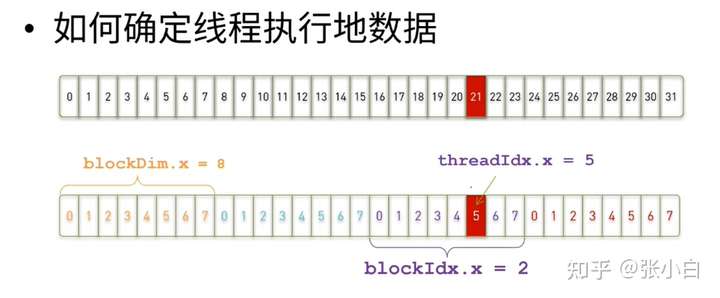
以上：假定每8个thread时一个block。

具体的公式如下：

具体的索引位置 index = blockDim.x * blockIdx.x + threadIdx.x

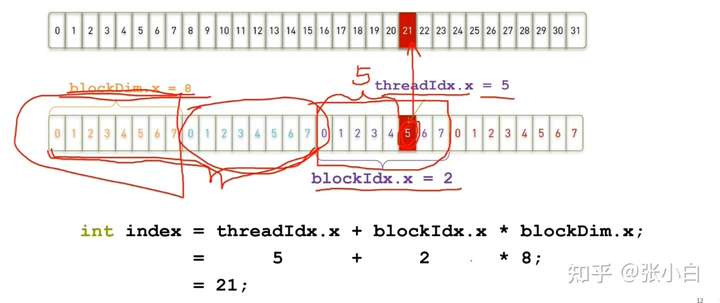
那么一个CUDA程序到底应该怎么写呢？

以将一个CPU实现的代码转换为GPU为例：

CPU的实现过程大致如下：

（1）主程序main：

先分配源地址空间a,b，目的地址空间c，并生成a，b的随机数。然后调用一维矩阵加的CPU函数。

（2）一维矩阵加的CPU函数：

遍历a,b地址空间，分别将 a[i] 与 b[i]相加，写入 c[i]地址。

这个时候，请注意是要显式地进行for循环遍历。

那么，GPU该如何实现呢？

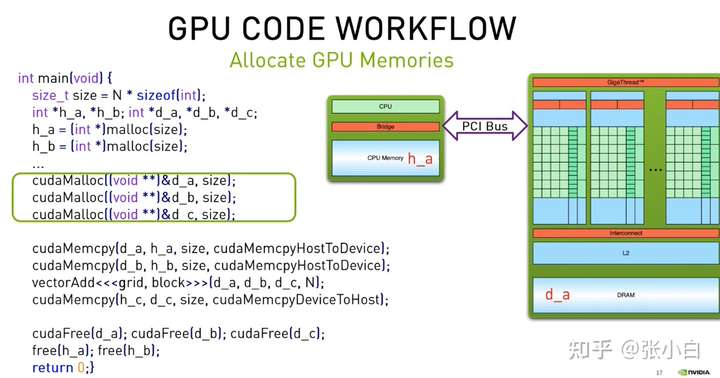
（1）主程序main：

因为GPU存在Host和Device内存，所以先申请host内存h_a,h_b，存放a，b的一维矩阵的内容（也可以生成随机数），并申请host内存h_c存放c的计算结果。

然后申请device内存，这个时候，需要申请 d_a,d_b两个源device内存(cudaMalloc)，以及d_c这个目的device内存(cudaMalloc)。将h_a和h_b的内容拷贝到d_a和d_b (显然需要使用 cudaMemcpyHostToDevice)；

然后调用核函数完成GPU的并行计算，结果写入h_c；

最后将d_c的device内存写回到h_c(cudaMemcpyDeviceToHost)，并释放所有的host内存(使用free)和device内存（使用cudaFree)。

（2）核函数

这里就是重点了。核函数只需要去掉最外层的循环，并且根据前面的index写法，将i替换成index的写法即可。

如何设置Gridsize和blocksize呢？

对于一维的情况：

block_size=128;

grid_size = (N+ block_size-1)/block_size;

（没有设成什么值是最好的）

每个block可以申请多少个线程呢？

总数也是1024。如（1024，1，1）或者（512，2，1）

grid大小没有限制。

每个block应该申请多少个线程呢？

底层是以warp为单位申请。如果blockDim为160，则正好申请5个warp。如果blockDim为161，则不得不申请6个warp。

如果数据过大，线程不够用怎么办？

这样子，每个线程需要处理多个数据。

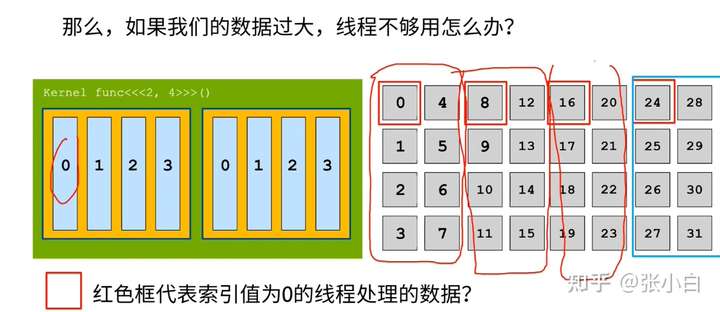
比如对于上图，线程0，需要处理 0,8,16,24 四个数据。核函数需要将每一个大块都跑一遍。代码如下：

这里引入了一个stride的概念，它的大小为blockDim.x X gridDim.x 。核函数需要完成每个满足 index = index + stride * count对应的相关地址的计算。

上午配套实验：

体验index：

Index_of_thread.cu

#include <stdio.h>

__global__ void hello_from_gpu()
{
   //仅仅是在昨天代码的基础上打印 blockIdx.x 和 threadIdx.x
    const int bid = blockIdx.x;
    const int tid = threadIdx.x;
    printf("Hello World from block %d and thread %d!\n", bid, tid);
}

int main(void)
{
    hello_from_gpu<<<5, 5>>>();
    
    //记得加上同步，不然结果会出不来。
    cudaDeviceSynchronize();
    return 0;
}

Makefile：

TEST_SOURCE = Index_of_thread.cu

TARGETBIN := ./Index_of_thread

CC = /usr/local/cuda/bin/nvcc

$(TARGETBIN):$(TEST_SOURCE)
	$(CC)  $(TEST_SOURCE) -o $(TARGETBIN)

.PHONY:clean
clean:
	-rm -rf $(TARGETBIN)

编译并执行：

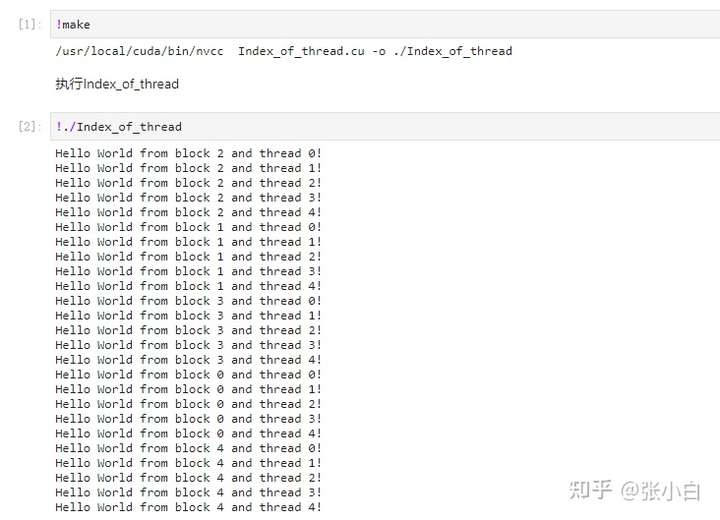
将 gridDim和blockDim改为 33,5，重新编译执行：

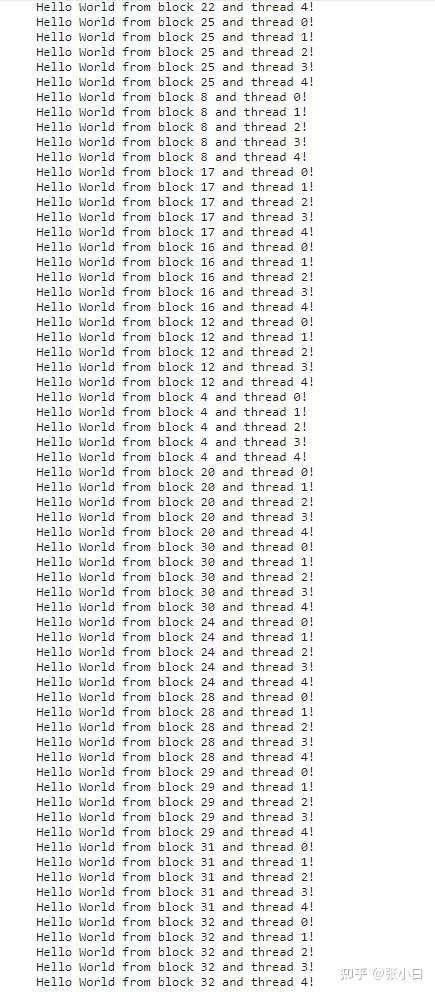
将 gridDim和blockDim改为 5,33，重新编译执行：

何老师让我们做这段的意义在于理解“1个warp是32个thread”的概念。有心的人可以通过nvprof分析下以上三个代码运行的速度对比。

完成一维向量计算：add

代码如下：

#include <math.h>
#include <stdio.h>

void __global__ add(const double *x, const double *y, double *z, int count)
{
    const int n = blockDim.x * blockIdx.x + threadIdx.x;
    
    //这里判断是防止溢出
	if( n < count)
	{
	    z[n] = x[n] + y[n];
	}

}
void check(const double *z, const int N)
{
    bool error = false;
    for (int n = 0; n < N; ++n)
    {
        //检查两个值是否相等，如不等则error=true.
        if (fabs(z[n] - 3) > (1.0e-10))
        {
            error = true;
        }
    }
    printf("%s\n", error ? "Errors" : "Pass");
}


int main(void)
{
    const int N = 1000;
    const int M = sizeof(double) * N;
    
    //分配host内存
    double *h_x = (double*) malloc(M);
    double *h_y = (double*) malloc(M);
    double *h_z = (double*) malloc(M);

    //初始化一维向量的值
    for (int n = 0; n < N; ++n)
    {
        h_x[n] = 1;
        h_y[n] = 2;
    }

    double *d_x, *d_y, *d_z;

    //分配device内存
    cudaMalloc((void **)&d_x, M);
    cudaMalloc((void **)&d_y, M);
    cudaMalloc((void **)&d_z, M);
    
    //host->device
    cudaMemcpy(d_x, h_x, M, cudaMemcpyHostToDevice);
    cudaMemcpy(d_y, h_y, M, cudaMemcpyHostToDevice);

    //这个是公式。记住就可以了。
    const int block_size = 128;
    const int grid_size = (N + block_size - 1) / block_size;
    
    //核函数计算
    add<<<grid_size, block_size>>>(d_x, d_y, d_z, N);

    //device->host
    cudaMemcpy(h_z, d_z, M, cudaMemcpyDeviceToHost);
    
    //检查结果
    check(h_z, N);

    //释放host内存
    free(h_x);
    free(h_y);
    free(h_z);
    
    //释放device内存
    cudaFree(d_x);
    cudaFree(d_y);
    cudaFree(d_z);
    return 0;
}

Makefile-add

TEST_SOURCE = vectorAdd.cu

TARGETBIN := ./vectorAdd

CC = /usr/local/cuda/bin/nvcc

$(TARGETBIN):$(TEST_SOURCE)
	$(CC)  $(TEST_SOURCE) -o $(TARGETBIN)

.PHONY:clean
clean:
	-rm -rf $(TARGETBIN)

执行编译：

查看性能：

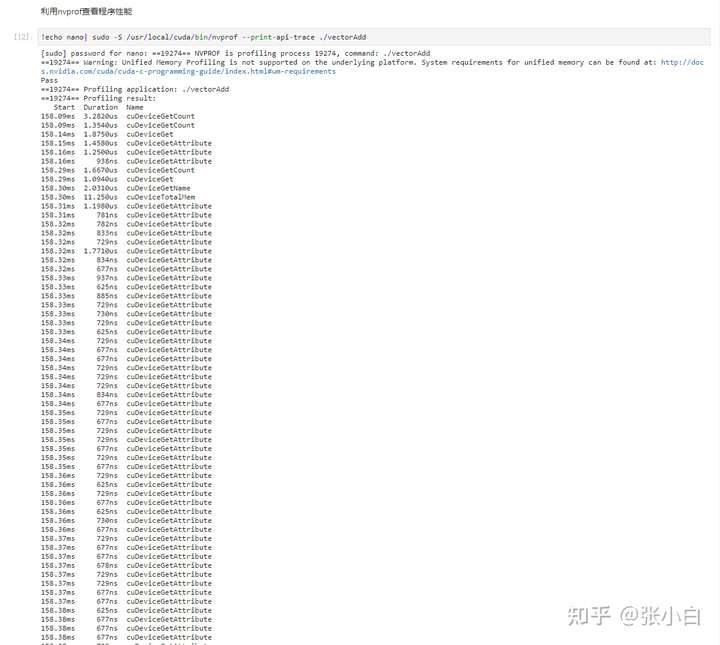
下午课件记录：

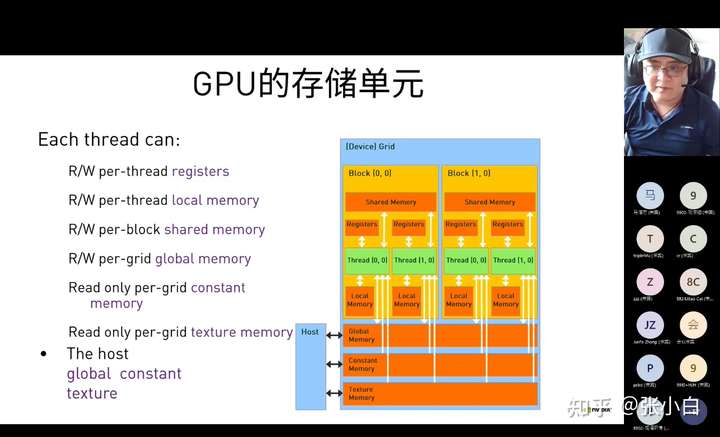
今天介绍global memory，就是GPU的显存。

在GPU上，on-board memory包含以下类型：

local memory 每个thread一个。线程私有。
global memory 每个grid一个。每个thread都可以读。
constant memory 每个grid一个。只读。每个thread都可以读。
texture memory 每个grid一个。只读。每个thread都可以读。

on-chip memory包含以下类型：

registers 每个thread一个。线程私有。
shared memory 每个block一个，一个block下所有线程都可以访问。

HOST内存函数

malloc 申请
memset 初始化
free 释放

DEVICE内存函数

cudaMalloc 申请
cudaMemset 初始化
cudaFree 释放

请注意，这里函数只返回状态。所以分配的内存地址作为函数参数。

HOST《-》DEVICE互相拷贝

cudaMemcpy( 目的内存地址，源内存地址，内存大小，cudaMemcpyHostToDevice/cudaMemcpyDeviceToHost/cudaMemcpyDeviceToDevice/cudaMemcpyHostToHost)

以矩阵乘为例:

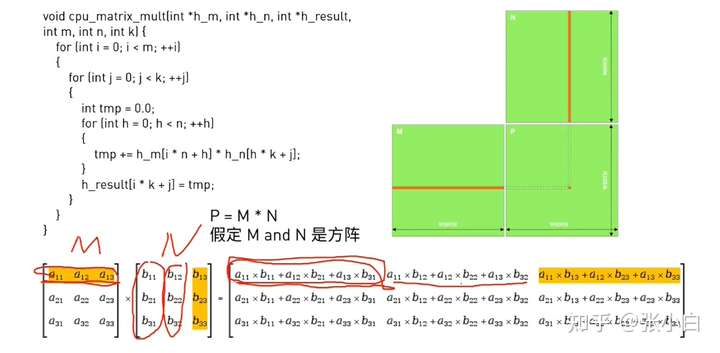
CPU的做法是嵌套循环，如上图所示。

GPU的做法应该是使用 index( blockIdx和 threadIdx的组合公式）替换原来的下标i,j。

这也是一般CUDA程序的套路——把for loop展开成每个线程处理其中的一步。

那么，如何使用CUDA将坐标拆开呢？将二维坐标（矩阵）改为在全局中的索引：需要找到每个线程需要处理元素的位置。

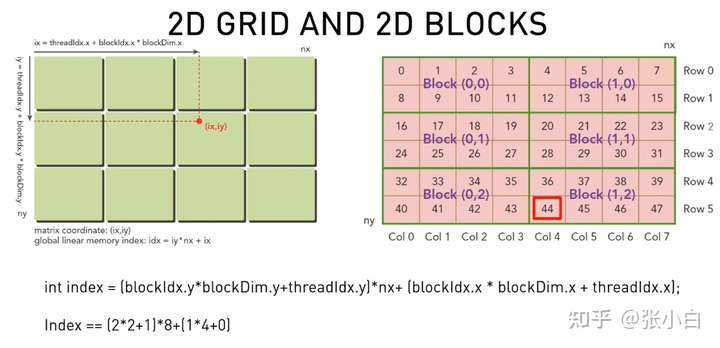
ty=线程在y方向的坐标

tx=线程在x方向的坐标

ty=blockIdx.y*blockDim.y + threadIdx.y

tx=blockIdx.x*blockDim.x + threadIdx.x

nx=x方向有多少数据。

index = ty * nx + tx

目的是将高维降为低维。

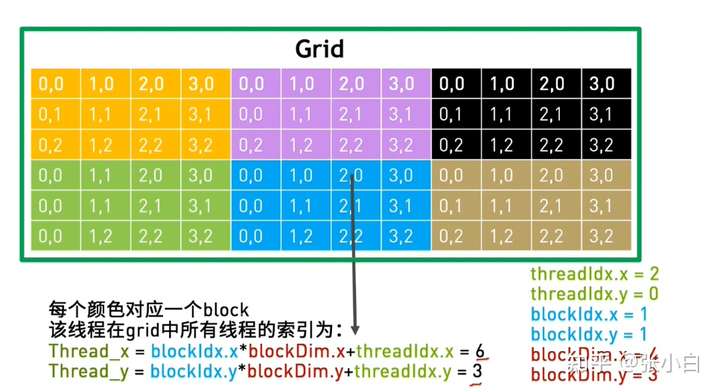
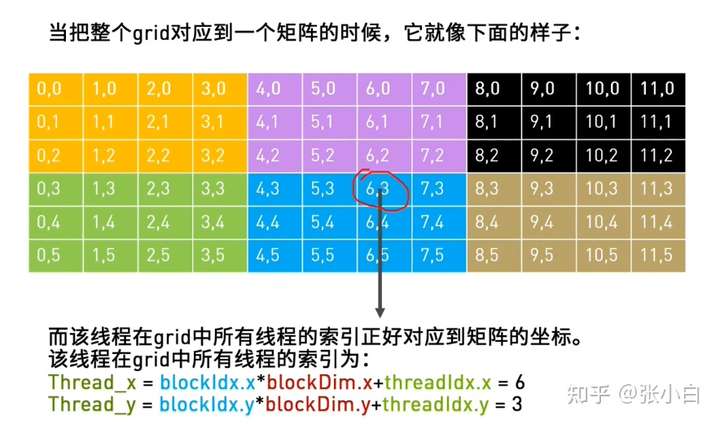
矩阵乘的每个核函数的算法如下：

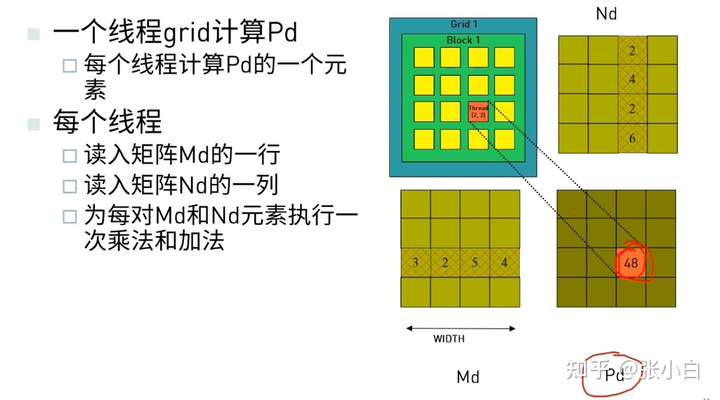
典型的核函数算法代码如下：

需要注意：

矩阵乘矩阵M是 mXn，矩阵N是 nXk，这里面需要矩阵M和矩阵N都有n。否则无法相乘。

上代码：

#include <stdio.h>
#include <math.h>

#define BLOCK_SIZE 16

//使用GPU进行矩阵计算
__global__ void gpu_matrix_mult(int *a,int *b, int *c, int m, int n, int k)
{ 
    int row = blockIdx.y * blockDim.y + threadIdx.y; 
    int col = blockIdx.x * blockDim.x + threadIdx.x;
    int sum = 0;
    if( col < k && row < m) 
    {
        for(int i = 0; i < n; i++) 
        {
            sum += a[row * n + i] * b[i * k + col];
        }
        c[row * k + col] = sum;
    }
} 

//使用CPU进行矩阵计算
void cpu_matrix_mult(int *h_a, int *h_b, int *h_result, int m, int n, int k) {
    for (int i = 0; i < m; ++i) 
    {
        for (int j = 0; j < k; ++j) 
        {
            int tmp = 0.0;
            for (int h = 0; h < n; ++h) 
            {
                tmp += h_a[i * n + h] * h_b[h * k + j];
            }
            h_result[i * k + j] = tmp;
        }
    }
}

int main(int argc, char const *argv[])
{
    /* 矩阵A mXn，矩阵B nXk --》矩阵乘计算的结果是 mXk */
    int m=3;
    int n=4;
    int k=5;

    int *h_a, *h_b, *h_c, *h_cc;
    
    //分配原矩阵的内存 h是host memory
    cudaMallocHost((void **) &h_a, sizeof(int)*m*n);
    cudaMallocHost((void **) &h_b, sizeof(int)*n*k);
    
    //分配 CPU结果内存
    cudaMallocHost((void **) &h_c, sizeof(int)*m*k);
    
    //分配 GPU结果内存
    cudaMallocHost((void **) &h_cc, sizeof(int)*m*k);


    //初始化矩阵A（mxn）
    srand(time(0));
    printf("---------------h_a------------------\n");
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) {
            h_a[i * n + j] = rand() % 1024;
            printf("%d",  h_a[i * n + j] );
            printf(" ");
        }
        printf("\n");
    }
    
 
    //初始化矩阵B（nxk）
    printf("---------------h_b------------------\n");
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < k; ++j) {
            h_b[i * k + j] = rand() % 1024;
            printf("%d",  h_b[i * k + j] );
            printf(" ");
        }
        printf("\n");
    }

    int *d_a, *d_b, *d_c;
    
    //分配 原矩阵的GPU内存 d是device memory
    cudaMalloc((void **) &d_a, sizeof(int)*m*n);
    cudaMalloc((void **) &d_b, sizeof(int)*n*k);
    
    //分配 目的矩阵的GPU内存
    cudaMalloc((void **) &d_c, sizeof(int)*m*k);

    // copy matrix A and B from host to device memory
    cudaMemcpy(d_a, h_a, sizeof(int)*m*n, cudaMemcpyHostToDevice);
    cudaMemcpy(d_b, h_b, sizeof(int)*n*k, cudaMemcpyHostToDevice);

    unsigned int grid_rows = (m + BLOCK_SIZE - 1) / BLOCK_SIZE;
    unsigned int grid_cols = (k + BLOCK_SIZE - 1) / BLOCK_SIZE;
    dim3 dimGrid(grid_cols, grid_rows);
    dim3 dimBlock(BLOCK_SIZE, BLOCK_SIZE);
   
    //GPU计算,结果放入h_c
    gpu_matrix_mult<<<dimGrid, dimBlock>>>(d_a, d_b, d_c, m, n, k);    

    cudaMemcpy(h_c, d_c, sizeof(int)*m*k, cudaMemcpyDeviceToHost);
    //cudaThreadSynchronize();

    //CPU计算，结果直接放入h_cc
    cpu_matrix_mult(h_a, h_b, h_cc, m, n, k);

    int ok = 1;
    for (int i = 0; i < m; ++i)
    {
        for (int j = 0; j < k; ++j)
        {
            // 比较大小的时候使用 a-b<0.0000000001 
            if(fabs(h_cc[i*k + j] - h_c[i*k + j])>(1.0e-10))
            {
                
                ok = 0;
            }
        }
    }
    
     printf("---------------h_c  cpu result------------------\n");
     for(int i=0;i<m;i++)
        {
            for(int j=0;j<k;j++)
            {
                //矩阵小的时候还可以打印，大的时候就别打了
                printf("%d",h_c[i*k + j] );
                printf(" ");
            }
           printf("\n");
        }
      
  
     printf("---------------h_cc gpu result----------------\n");
     for(int i=0;i<m;i++)
        {
            for(int j=0;j<k;j++)
            {
                //矩阵小的时候还可以打印，大的时候就别打了
                printf("%d",h_cc[i*k + j] );
                printf(" ");
            }
           printf("\n");
        }
      

    if(ok)
    {
       
        printf("Pass!!!\n");
    }
    else
    {
        printf("Error!!!\n");
    }

    // free memory
    cudaFree(d_a);
    cudaFree(d_b);
    cudaFree(d_c);
    cudaFreeHost(h_a);
    cudaFreeHost(h_b);
    cudaFreeHost(h_c);
    return 0;
}

代码中张小白加上了注释，已经介绍得比较清楚了。

我们执行下看看：

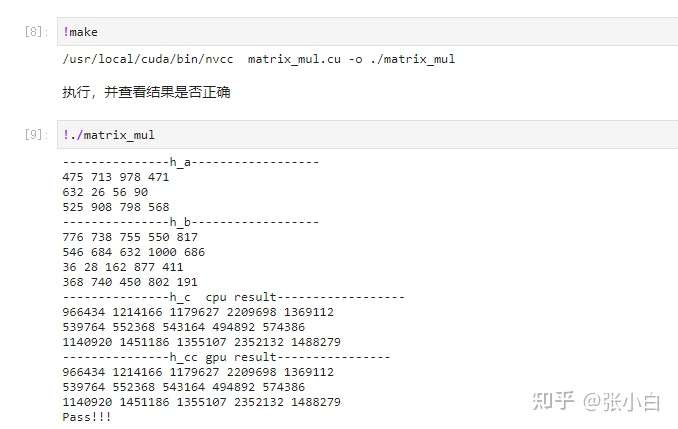
代码以 3X4和4X5的矩阵相乘，得到了3X5的矩阵结果。

这个结果跟CPU计算的结果做了对比。显示Pass表示结果是一致的（其实张小白把两个结果都打印的出来，当然也是一致的）

这里面有个小TIPS，就是在调用rand()生成随机数的时候，可以使用srand(time(0)) 做随机数种子，这样下次调用的时候跟这次生成的内容就会不一样。如果去掉这句话，每次执行的结果都是一样的。

（未完待续）

点赞
收藏
关注作者

0/1000

抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认取消

加入云驻计划，成为创作者

华为云周边好礼
免费体验产品
特殊身份标识
线下官方门票
内部专家零距离
与10000+优质创作者共同成长

立即加入

2022CUDA夏季训练营Day2实践

上午配套实验：

完成一维向量计算：add

下午课件记录：

全部回复

设置昵称

关于作者

目录

加入云驻计划，成为创作者

2022CUDA夏季训练营Day2实践

上午配套实验：

完成一维向量计算：add

下午课件记录：

全部回复

设置昵称

关于作者

目录

加入云驻计划，成为创作者

推荐阅读

相关产品