【图像融合】基于matlab小波变换遥感图像融合【含Matlab源码 744期】

一、获取代码方式

获取代码方式1：
通过订阅紫极神光博客付费专栏，凭支付凭证，私信博主，可获得此代码。

获取代码方式2：
完整代码已上传我的资源：【图像融合】基于matlab小波变换遥感图像融合【含Matlab源码 744期】

备注：
订阅紫极神光博客付费专栏，可免费获得1份代码（有效期为订阅日起，三天内有效）；

二、小波变换图像融合技术简介

1 案例背景
图像融合，指通过对同一目标或同一场景用不同的传感器(或用同一传感器采用不同的方式)进行图像采集得到多幅图像，对这些图像进行合成得到单幅合成图像，而该合成图像是单传感器无法采集得到的。图像融合所输出的合成图像往往能够保持多幅原始图像中的关键信息，进而为对目标或场景进行更精确、更全面的分析和判断提供条件。图像融合属于数据融合范畴，是数据融合的子集，兼具数据融合和图像可视化的优点。因此，图像融合能够在一定程度上提高传感器系统的有效性和信息的使用效率，进而提高待分析目标的分辨率，抑制不同传感器所产生的噪声，改善图像处理的效果。
图像融合最早是以数据融合理论为基础的，通过计算像素算术平均的方式得到合成图像。该方法忽略了像素间的相互关系，往往会产生融合图像的对比度差、可视化效果不理想等问题。因此，为了提高目标检测的分辨率，抑制不同传感器的检测噪声，本案例选择了一种基于小波变换的图像数据融合方法，首先通过小波变换将图像分解到高频、低频，然后分别进行融合处理，最后再逆变换到图像矩阵"。在融合过程中，为了尽可能保持多源图像的特征，在小波分解的高频域内，选择图像邻域平均绝对值较大的系数作为融合小波重要系数；在小波分解的低频域内，选择对多源图像的低频系数进行加权平均作为融合小波近似系数。在反变换过程中，利用重要小波系数和近似小波系数作为输入进行小波反变换。在融合图像输出后，对其做进一步的处理。实验结果表明，基于小波变换的图像数据融合方法运行效率高，具有良好的融合效果，并可用于广泛的研究领域，具有一定的使用价值。
根据融合的作用对象，图像融合一般可以分为3个层次：像素级图像融合、特征级图像融合和决策级图像融合。其中，像素级融合是作用于图像像素点最底层的融合，本章所研究的图像融合是像素级图像融合。

1.2理论基础
传统的直接像素算术平均进行图像融合的方法往往会造成融合结果对比度降低、可视化效果不理想等问题，为此研究人员提出了基于金字塔的图像融合方法，其中包括拉普拉斯金字塔、梯度金字塔等多分辨率融合方法。20世纪80年代中期发展起来的小波变换技术为图像融合提供了新的工具，小波分解的紧致性、对称性和正交性使其相对于金字塔分解具有更好的图像融合性能。此外，小波变换具有“数学显微镜”聚焦的功能，能实现时间域和频率域的步调统一，能对频率域进行正交分解，因此小波变换在图像处理中具有非常广泛的应用，已经被运用到图像处理的几乎所有分支，如图像融合、边缘检测、图像压缩、图像分割等领域。
假设对一维连续小波w…(t)和连续小波变换W，(a，b)进行离散化，其中，a表示尺度参数， b表示平移参数， 在离散化过程中分别取a=a{和b=bf， 其中， jeZ， a， >1，则对应的离散小波函数如下：

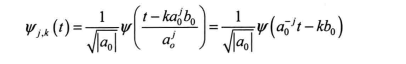
离散化的小波变换系数如下：

小波重构公式如下：

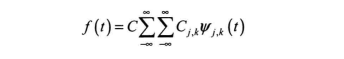
式中，C为常数且与数据信号无关。根据对连续函数进行离散化逼近的步骤，如果选择的a， 和b， 越小， 则生成的网格节点就越密集， 所计算的离散小波函数wj x® 和离散小波系数Cj就越多，进而数据信号重构的精确度也越高。
由于数字图像是二维矩阵，所以需要将一维信号的小波变换推广到二维信号。假设(x)是一个一维的尺度函数，p(x)是相应的小波函数，那么可以得到一个二维小波变换的基础函数：
v’(x，y)=0(x)v(y)w(x，y)=y(x)(y)v(x，y)=V(x)w(y)
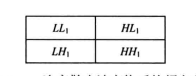
由于数字图像是二维矩阵， 一般假设图像矩阵的大小为NxN， 且N=2"(n为非负整数)，所以经一层小波变换后，原始图像便分解为4个分辨率为原来尺寸一的子带区域，如图11-1所示，分别包含了相应频带的小波系数，这一过程相当于在水平方向和垂直方向上进行隔点采样。

进行下一层小波变换时，变换数据集中在LL子带上。说明了图像小波变换的数学原型。
(1)LL频带保持了原始图像的内容信息，图像的能量集中于此频带：

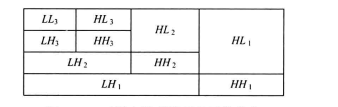
对图像进行小波变换的原理就是通过低通滤波器和高通滤波器对图像进行卷积滤波，再进行二取一的下抽样。因此，图像通过一层小波变换可以被分解为1个低频子带和3个高频子带。其中，低频子带LL；通过对图像水平方向和垂直方向均进行低通滤波得到；高频子带HL通过对图像水平方向高通滤波和垂直方向低通滤波得到；高频子带LH通过对图像水平方向低通滤波和垂直方向高通滤波得到：高频子带HH通过对图像水平方向高通滤波和垂直方向高通滤波得到。各子带的分辨率为原始图像的，同理，对图像进行二层小波变换时只对低频子带LL进行， 可以将LLi子带分解为LL 2、LH 2、HL 2和HH， 各子带的分辨率为原始图像的一。，以此类推可得到三层及更高层的小波变换结果。所以，进行
一层小波变换得到4个子带，进行二层小波变换得到7个子带，进行x层分解就得到3·x+1个子带。如图11-2所示为三层小波变换后的系数分布。

三、部分源代码

clc;
clear all;
close all;

Panc = imread('high.jpg');
Mult = imread('low.jpg');
figure;
subplot(1,2,1),imshow(Panc);title('高分辨率影像');
subplot(1,2,2),imshow(Mult);title('多波段影像');

Mult_R = Mult(:,:,1);
Mult_G = Mult(:,:,2);
Mult_B = Mult(:,:,3);

% 高分辨率全色图小波变换
[CPanc,LPanc] = wavedec2(Panc,3,'db13');
WH = LPanc(1,:);
length = WH(1)*WH(2);

[CMult_R,LMult_R] = wavedec2(Mult_R,3,'db13' ); % R通道小波变换，得到的低频替换全色图的低频系数
CR = CPanc; CR(1:length) = CMult_R(1:length);

[CMult_G,LMult_G] = wavedec2(Mult_G,3,'db13' ); % G通道小波变换，得到的低频替换全色图的低频系数
CG = CPanc; CG(1:length) = CMult_G(1:length);   

[CMult_B,LMult_B] = wavedec2(Mult_B,3,'db13' ); % B通道小波变换，得到的低频替换全色图的低频系数
CB = CPanc; CB(1:length) = CMult_B(1:length);

% 低频为多光谱图的低频系数，高频为全色图的高频系数，进行小波重构
Img_Result(:,:,1) = waverec2(CR,LPanc,'db13' );
Img_Result(:,:,2) = waverec2(CG,LPanc,'db13' );
Img_Result(:,:,3) = waverec2(CB,LPanc,'db13' );

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
  
21
  
22
  
23
  
24
  
25
  
26
  
27
  
28
  
29
  
30
  
31
  
32
 

四、运行结果

五、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 蔡利梅.MATLAB图像处理——理论、算法与实例分析[M].清华大学出版社，2020.
[2]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社，2013.
[3]周品.MATLAB图像处理与图形用户界面设计[M].清华大学出版社，2013.
[4]刘成龙.精通MATLAB图像处理[M].清华大学出版社，2015.

文章来源: qq912100926.blog.csdn.net，作者：海神之光，版权归原作者所有，如需转载，请联系作者。

原文链接：qq912100926.blog.csdn.net/article/details/115558017