LeetCode-654. 最大二叉树

题目描述：

给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的 最大二叉树 定义如下：

二叉树的根是数组 nums 中的最大元素。
左子树是通过数组中 最大值左边部分 递归构造出的最大二叉树。
右子树是通过数组中 最大值右边部分 递归构造出的最大二叉树。
返回有给定数组 nums 构建的 最大二叉树 。

示例：

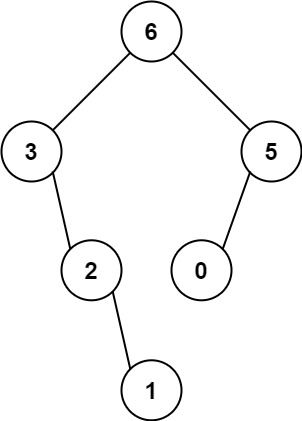
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

思路分析：

本方法非常简单。创建方法 construct(nums, l, r)，用于找出在数组 nums 中从 l到 r 索引（不包含第 r 个位置）中最大二叉树的根节点。

算法步骤如下：

首先调用 construct(nums, 0, n)，其中 n 是数组 nums 的长度。

在索引范围 (l:r-1)内找到最大值的索引，将 nums[max_i] 作为根节点。

调用 construct(nums, l, max_i) 创建根节点的左孩子。递归执行此操作，创建根节点的整个左子树。

类似的，调用 construct(nums, max_i + 1, r) 创建根节点的右子树。

方法 construct(nums, 0, n) 返回最大二叉树的根节点。

代码实现：

public class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return construct(nums, 0, nums.length);
    }
    public TreeNode construct(int[] nums, int l, int r) {
        if (l == r)
            return null;
        int max_i = max(nums, l, r);
        TreeNode root = new TreeNode(nums[max_i]);
        root.left = construct(nums, l, max_i);
        root.right = construct(nums, max_i + 1, r);
        return root;
    }
    public int max(int[] nums, int l, int r) {
        int max_i = l;
        for (int i = l; i < r; i++) {
            if (nums[max_i] < nums[i])
                max_i = i;
        }
        return max_i;
    }
}

文章来源: blog.csdn.net，作者：小小谢先生，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/xiewenrui1996/article/details/113940073