LeetCode-144：二叉树的前序遍历

题目描述：

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

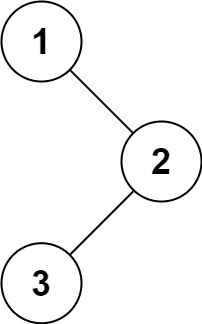
输入：root = [1,null,2,3]
输出：[1,2,3]

思路分析：

递归或是迭代实现。

递归：

首先我们需要了解什么是二叉树的前序遍历：按照访问根节点——左子树——右子树的方式遍历这棵树，而在访问左子树或者右子树的时候，我们按照同样的方式遍历，直到遍历完整棵树。因此整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程。

定义 preorder(root) 表示当前遍历到 root 节点的答案。按照定义，我们只要首先将 root 节点的值加入答案，然后递归调用 preorder(root.left) 来遍历 root 节点的左子树，最后递归调用 preorder(root.right) 来遍历 root 节点的右子树即可，递归终止的条件为碰到空节点。

  

   

    

     

    
    

     

      class Solution {
     
    
   

    

     

    
    

     
    public List<Integer> preorderTraversal(TreeNode root) {
     
    
   

    

     

    
    

     

              List<Integer> res = new ArrayList<Integer>();
     
    
   

    

     

    
    

     

              preorder(root, res);
     
    
   

    

     

    
    

     
        return res;
     
    
   

    

     

    
    

     

          }
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
    public void preorder(TreeNode root, List<Integer> res) {
     
    
   

    

     

    
    

     
        if (root == null) {
     
    
   

    

     

    
    

     
            return;
     
    
   

    

     

    
    

     

              }
     
    
   

    

     

    
    

     

              res.add(root.val);
     
    
   

    

     

    
    

     

              preorder(root.left, res);
     
    
   

    

     

    
    

     

              preorder(root.right, res);
     
    
   

    

     

    
    

     

          }
     
    
   

    

     

    
    

     

      }
     
    
  
 

时间复杂度：O(n)O(n)，其中 nn 是二叉树的节点数。每一个节点恰好被遍历一次。

空间复杂度：O(n)O(n)，为递归过程中栈的开销，平均情况下为 O(\log n)O(logn)，最坏情况下树呈现链状，为 O(n)O(n)。

迭代：

本质上是在模拟递归，因为在递归的过程中使用了系统栈，所以在迭代的解法中常用Stack来模拟系统栈。

  

   

    

     

    
    

     

      class Solution {
     
    
   

    

     

    
    

     
    public List<Integer> preorderTraversal(TreeNode root) {
     
    
   

    

     

    
    

     

              List<Integer> res = new ArrayList<Integer>();
     
    
   

    

     

    
    

     
        if (root == null) {
     
    
   

    

     

    
    

     
            return res;
     
    
   

    

     

    
    

     

              }
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

              Deque<TreeNode> stack = new LinkedList<TreeNode>();
     
    
   

    

     

    
    

     
        TreeNode node = root;
     
    
   

    

     

    
    

     
        while (!stack.isEmpty() || node != null) {
     
    
   

    

     

    
    

     
            while (node != null) {
     
    
   

    

     

    
    

     

                      res.add(node.val);
     
    
   

    

     

    
    

     

                      stack.push(node);
     
    
   

    

     

    
    

     

                      node = node.left;
     
    
   

    

     

    
    

     

                  }
     
    
   

    

     

    
    

     

                  node = stack.pop();
     
    
   

    

     

    
    

     

                  node = node.right;
     
    
   

    

     

    
    

     

              }
     
    
   

    

     

    
    

     
        return res;
     
    
   

    

     

    
    

     

          }
     
    
   

    

     

    
    

     

      }
     
    
  
 

时间复杂度：O(n)O(n)，其中 nn 是二叉树的节点数。每一个节点恰好被遍历一次。

空间复杂度：O(n)O(n)，为迭代过程中显式栈的开销，平均情况下为 O(\log n)O(logn)，最坏情况下树呈现链状，为 O(n)O(n)。

文章来源: blog.csdn.net，作者：小小谢先生，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/xiewenrui1996/article/details/113524388