【数据结构与算法】之深入解析“整数反转”的求解思路与算法示例

一、题目要求

• 给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。
• 如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ，就返回 0。
• 假设环境不允许存储 64 位整数（有符号或无符号）。
• 示例 1：

输入：x = 123
输出：321

  

 

  
1
  
2
 

• 示例 2：

输入：x = -123
输出：-321

  

 

  
1
  
2
 

• 示例 3：

输入：x = 120
输出：21

  

 

  
1
  
2
 

• 示例 4：

输入：x = 0
输出：0

  

 

  
1
  
2
 

• 提示：-231 <= x <= 231 - 1。

二、求解算法

① 末尾数字

• 首先我们想一下，怎么去反转一个整数？用栈？还是把整数变成字符串，再去反转这个字符串？这两种方式是可以，但其实并不是太好，实际上我们只要能拿到这个整数的“末尾数字”就可以。
• 以 12345 为例，先拿到 5，再拿到 4，之后是 3，2，1，按这样的顺序就可以反向拼接处一个数字了，也就能达到反转的效果。
• 那么，怎么拿末尾数字呢？其实很简单，用取模运算就可以了，如下图所示：

• 分析说明：
• • 将 12345 % 10 得到 5，之后将 12345 / 10；
• • 将 1234 % 10 得到 4，再将 1234 / 10；
• • 将 123 % 10 得到 3，再将 123 / 10；
• • 将 12 % 10 得到 2，再将 12 / 10；
• • 将 1 % 10 得到 1，再将 1 / 10。
• 这么看起来，一个循环就搞定了，循环的判断条件是 x>0。但细细一想，这样不对，因为忽略了负数，循环的判断条件应该是 while(x!=0)，无论正数还是负数，按照上面不断的 /10 这样的操作，最后都会变成 0，所以判断终止条件就是 !=0，有了取模和除法操作，对于像 12300 这样的数字，也可以完美的解决掉了。
• 看起来这道题就这么解决了，但请注意，题目上还有这么一句：假设我们的环境只能存储得下 32 位的有符号整数，则其数值范围为 [−2³, 2³¹ − 1]。
• 也就是说我们不能用 long 存储最终结果，而且有些数字可能是合法范围内的数字，但是反转过来就超过范围了。假设有 1147483649 这个数字，它是小于最大的 32 位整数 2147483647 的，但是将这个数字反转过来后就变成了 9463847411，这就比最大的 32 位整数还要大了，这样的数字是没法存到 int 里面的，所以肯定要返回 0(溢出了)。甚至，还需要提前判断。
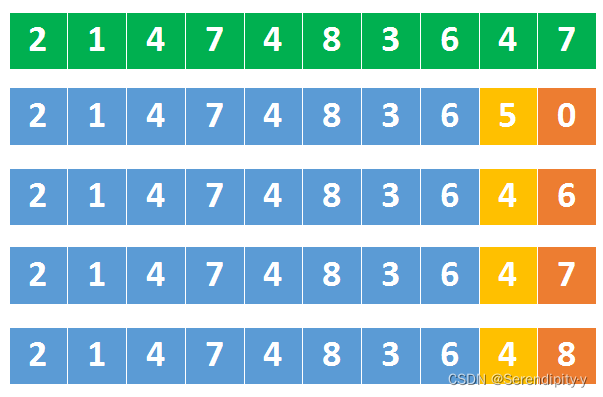
• 如下图所示：
• • 绿色部分是最大 32 位整数；
• • 第二排数字中，橘色是 5，它是大于上面同位置的 4，这就意味着 5 后跟任何数字，都会比最大 32 为整数都大。
• 所以到【最大数的1/10】时，就要开始判断：
• • • 如果某个数字大于 214748364，那后面就不用再判断，肯定溢出；
• • • 如果某个数字等于 214748364，这对应到图中第三、第四、第五排的数字，需要要跟最大数的末尾数字比较，如果这个数字比 7 还大，说明溢出。
• • 对于负数也是一样的。

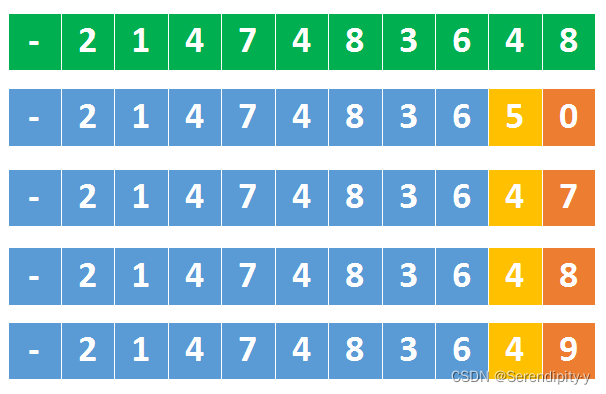
• 再如下所示：
• • 绿色部分是最小的 32 位整数，同样是在【最小数的 1/10】时开始判断；
• • 如果某个数字小于 -214748364 说明溢出；
• • 如果某个数字等于 -214748364，还需要跟最小数的末尾比较，即看它是否小于 8。

• Java 示例：

class Solution {
    public int reverse(int x) {
        int res = 0;
        while(x!=0) {
            // 每次取末尾数字
            int tmp = x%10;
            // 判断是否 大于 最大32位整数
            if (res>214748364 || (res==214748364 && tmp>7)) {
                return 0;
            }
            // 判断是否 小于 最小32位整数
            if (res<-214748364 || (res==-214748364 && tmp<-8)) {
                return 0;
            }
            res = res*10 + tmp;
            x /= 10;
        }
        return res;
    }
}			

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
  
16
  
17
  
18
  
19
  
20
 

② 数学推导（LeetCode 官方解法）

• 记 rev 为翻转后的数字，为完成翻转，可以重复「弹出」x 的末尾数字，将其「推入」rev 的末尾，直至 x 为 0。
• 要在没有辅助栈或数组的帮助下「弹出」和「推入」数字，可以使用如下数学方法：

// 弹出 x 的末尾数字 digit
digit = x % 10
x /= 10

// 将数字 digit 推入 rev 末尾
rev = rev * 10 + digit

  

 

  
1
  
2
  
3
  
4
  
5
  
6
 

• 题目需要判断反转后的数字是否超过 32 位有符号整数的范围 [−2³¹,2³¹−1]，例如 x=2123456789 反转后的rev=9876543212>2³¹−1=2147483647，超过了 32 位有符号整数的范围。
• 因此需要在「推入」数字之前，判断是否满足：

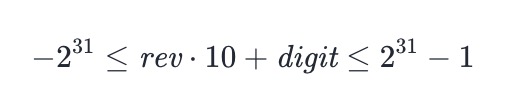
• 若该不等式不成立则返回 0。但是题目要求不允许使用 64 位整数，即运算过程中的数字必须在 32 位有符号整数的范围内，因此不能直接按照上述式子计算，需要另寻他路。
• 考虑 x>0 的情况，记 INT_MAX=2³¹−1=2147483647，由于：

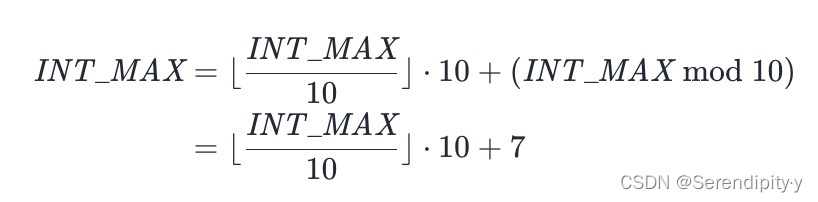
• 则不等式：

• 等价于：

• 移项得：

• 讨论该不等式成立的条件：

• 注意到当 rev= INT_MAX/10 时若还能推入数字，则说明 x 的位数与 INT_MAX 的位数相同，且要推入的数字 digit 为 x 的最高位。由于 x 不超过 INT_MAX，因此 digit 不会超过 INT_MAX 的最高位，即 digit≤2。所以实际上当 rev= INT_MAX/10 时不等式必定成立。
• 因此判定条件可简化为：当且仅当 rev≤INT_MAX/10 时，不等式成立，x<0 的情况类似，不再赘述。
• 综上所述，判断不等式：

• 是否成立，可改为判断不等式：

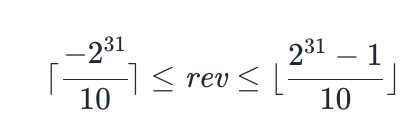
• 是否成立，若不成立则返回 0。
• C++ 示例：

class Solution {
public:
    int reverse(int x) {
        int rev = 0;
        while (x != 0) {
            if (rev < INT_MIN / 10 || rev > INT_MAX / 10) {
                return 0;
            }
            int digit = x % 10;
            x /= 10;
            rev = rev * 10 + digit;
        }
        return rev;
    }
};

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
  
15
 

• Java 示例：

class Solution {
    public int reverse(int x) {
        int rev = 0;
        while (x != 0) {
            if (rev < Integer.MIN_VALUE / 10 || rev > Integer.MAX_VALUE / 10) {
                return 0;
            }
            int digit = x % 10;
            x /= 10;
            rev = rev * 10 + digit;
        }
        return rev;
    }
}

  

 

  
1
  
2
  
3
  
4
  
5
  
6
  
7
  
8
  
9
  
10
  
11
  
12
  
13
  
14
 

文章来源: blog.csdn.net，作者：Serendipity·y，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/Forever_wj/article/details/122217169