【数据结构与算法】之深入解析“不同路径II”的求解思路与算法示例
【摘要】
一、题目要求
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” ),机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)...
一、题目要求
- 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” ),机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。现在考虑网格中有障碍物,那么从左上角到右下角将会有多少条不同的路径?
- 网格中的障碍物和空位置分别用 1 和 0 来表示。
- 示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
- 1
- 2
- 3
- 4
- 5
- 6
- 示例 2:

输入:obstacleGrid = [[0,1],[0,0]]
输出:1
- 1
- 2
- 提示:
-
- m == obstacleGrid.length;
-
- n == obstacleGrid[i].length;
-
- 1 <= m, n <= 100;
-
- obstacleGrid[i][j] 为 0 或 1。
二、求解算法
① 递归
- 如果是没有障碍物的话,从 (0,0) 出发,每次只能往下走、或者往右走。假设 i 表示行、j 表示列,当前点为 (i,j),那么每次只能往 (i + 1, j) 移动、或者往 (i, j + 1) 移动,递归方向:
-
- 往右:i 不动,j+1;
-
- 往下:j+1,i 不动;
- 对于有障碍物的情况下怎么办呢?其实也简单,直接返回 0 就可以了,这表能走到障碍物的路径总和为 0:
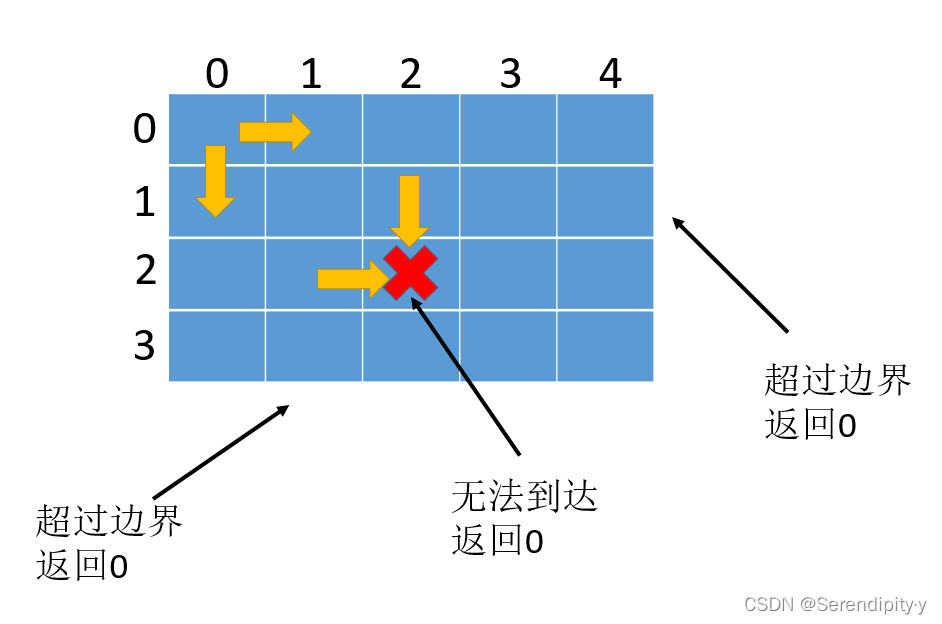
- 有了上述条件,递归就很容易了,每次往右、或者往下走,到达边界条件返回 0,到达终点返回 1,如下所示,橙色的 (2,2) 这个点,表示从这里发出到达终点有多少路径:
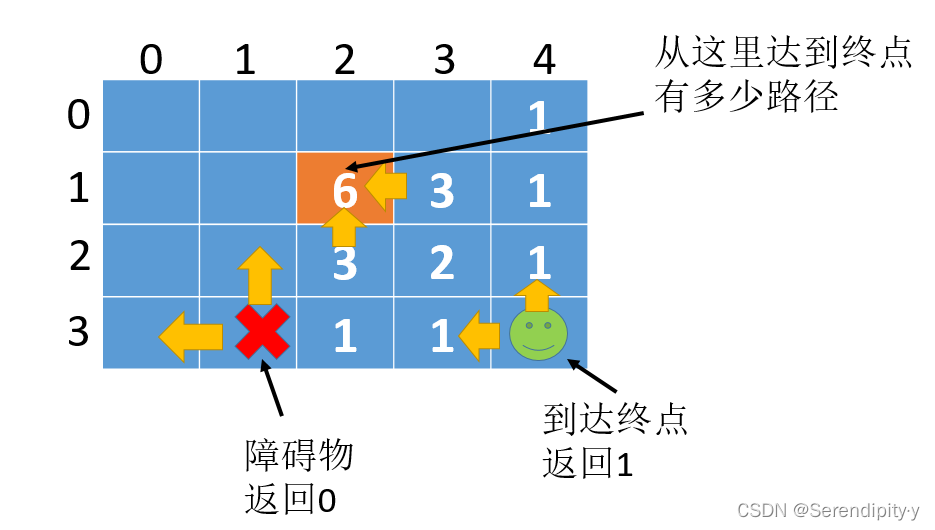
- 同理,(0,0) 就是从起点出发,走到终点有多少路径,也就是题目的要求。
- Java 示例:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
return dfs(new HashMap<Pair,Integer>(), obstacleGrid, 0, 0);
}
private int dfs(Map<Pair,Integer> cache, int[][] arr, int i, int j) {
Pair p = new Pair(i,j);
if(cache.containsKey(p)) {
return cache.get(p);
}
// 边界/障碍物检查
if(i >= arr.length || j >= arr[0].length || arr[i][j] == 1) {
return 0;
}
// 达到终点
if(i == arr.length - 1 && j == arr[0].length - 1) {
return 1;
}
// 继续往右(i,j+1)、往下(i+1,j)递归调用
int res = dfs(cache, arr, i + 1, j) + dfs(cache, arr, i, j + 1);
cache.put(p, res);
return res;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
② 动态规划 1
- 对于动态规划,反过来想,如何到达下图中橙色的 (2,2) 这个点呢?只能从上方和左方到达 (2,2) 这个点,到达障碍物 (3,2) 这个点的路径总和为 0:
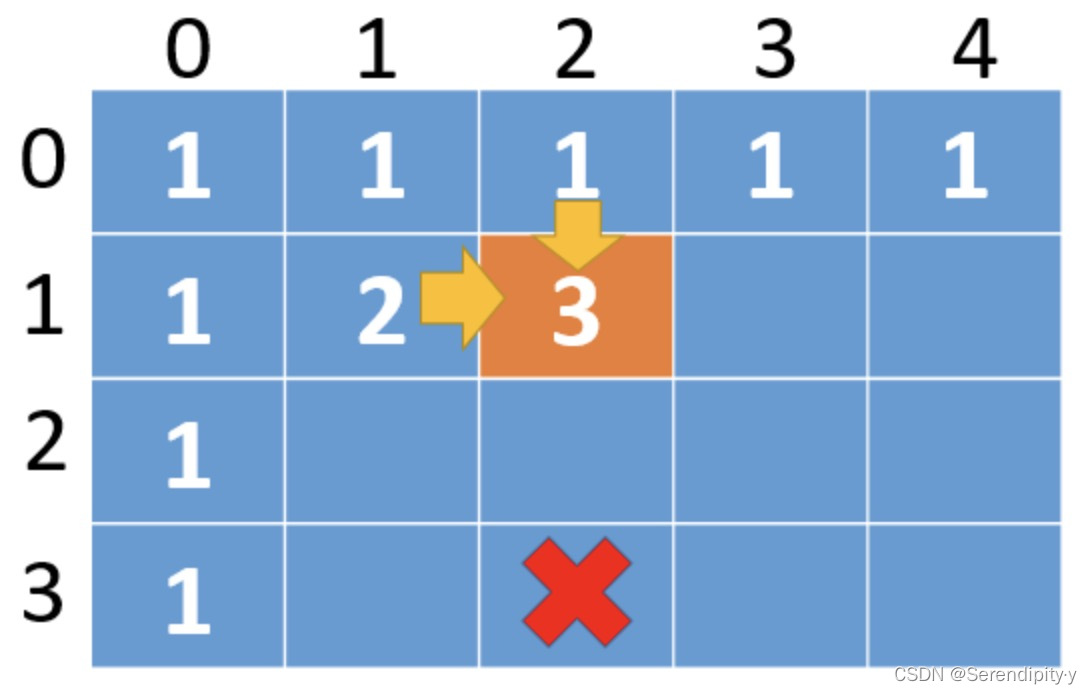
- 只能由两个方向而来,上方、或者是左方;对于 (3,2) 障碍物这个点来说,能到达这里的路径就是 0,因此对于 (i,j) 这个点来说,其动态规划转移方程就是:
if 当前点不是障碍物:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
else:
dp[i][j] = 0
- 1
- 2
- 3
- 4
- 还需要处理下边界情况,也就是第一列、第一行时,如下图,只要第一列中的某个格子是障碍物,那么这个格子跟后面的都无法到达:
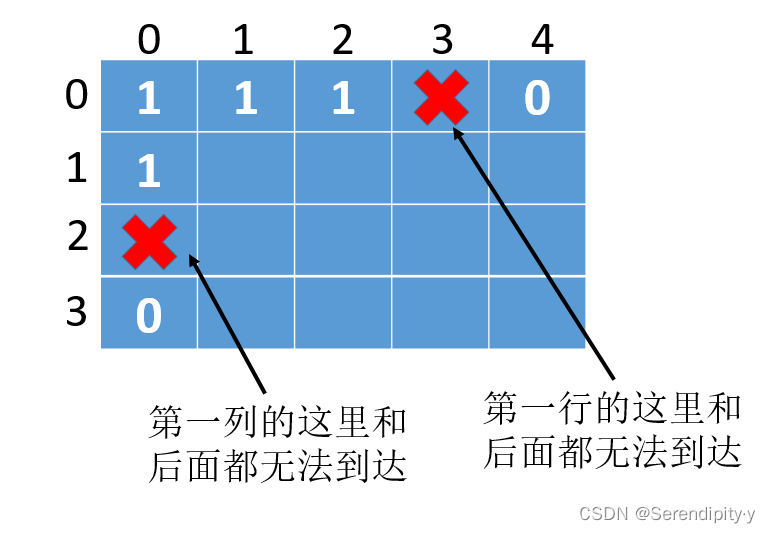
- 同理,第一行中如果有格子是障碍物,那么这个格子跟后面的都无法到达。
- Java 示例:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int n = obstacleGrid.length;
int m = obstacleGrid[0].length;
int[][] dp = new int[n][m];
// (0,0)这个格子可能有障碍物
dp[0][0] = (obstacleGrid[0][0] == 1) ? 0 : 1;
// 处理第一列
for(int i = 1; i < n; ++i) {
if(obstacleGrid[i][0] == 1 || dp[i - 1][0] == 0) {
dp[i][0] = 0;
} else {
dp[i][0] = 1;
}
}
// 处理第一行
for(int j = 1; j < m; ++j) {
if(obstacleGrid[0][j] == 1 || dp[0][j - 1] == 0) {
dp[0][j] = 0;
} else {
dp[0][j] = 1;
}
}
for(int i = 1; i < n; ++i) {
for(int j = 1; j < m; ++j) {
// 如果当前格子是障碍物
if(obstacleGrid[i][j] == 1) {
dp[i][j] = 0;
// 路径总数来自于上方(dp[i-1][j])和左方(dp[i][j-1])
} else {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[n - 1][m - 1];
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
③ 动态规划 2
- 跟动态规划 1 解法正好是反过来的,动态规划 1 解法中,是从 (0,0) 走到 (n-1,m-1),动态规划 2 中,是从 (n-1,m-1) 走到 (0,0)。因此反过来推导,对于 (2,2) 这个点,只能从下方、右方转移过来:
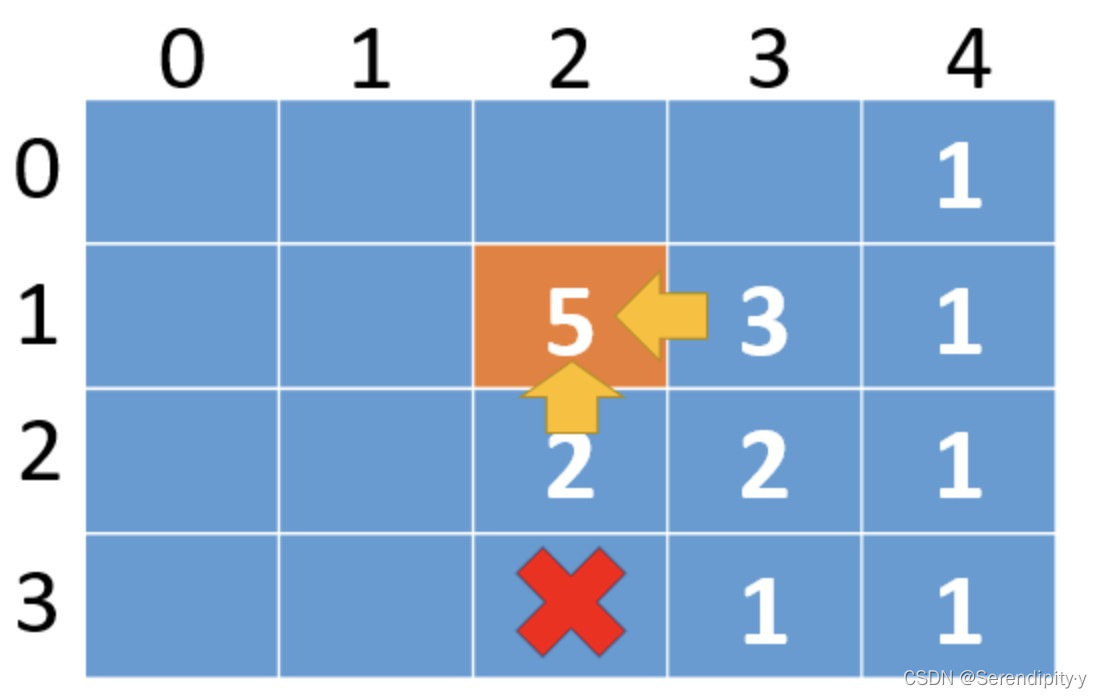
- 同样,反着推的时候也需要处理下边界问题,也就是最后一行,最后一列需要单独处理一下。这里的思路跟前一种解法是一样的,只是倒退来的:
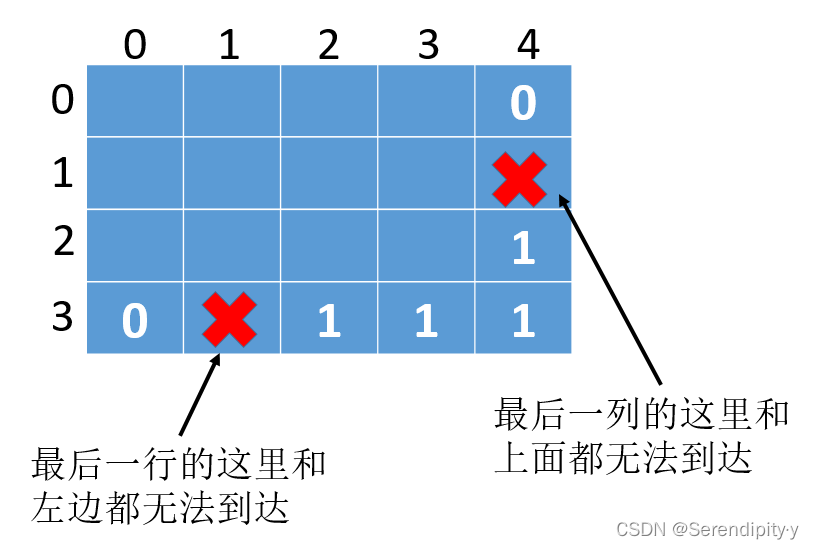
- Java 示例:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int n = obstacleGrid.length;
int m = obstacleGrid[0].length;
int[][] dp = new int[n][m];
// 判断终点是否有障碍物
dp[n - 1][m - 1] = (obstacleGrid[n - 1][m - 1] == 1) ? 0 : 1;
// 处理最后一列
for(int i = n -2; i >=0; --i) {
if(obstacleGrid[i][m - 1] == 1 || dp[i + 1][m - 1] == 0) {
dp[i][m - 1] = 0;
} else {
dp[i][m - 1] = 1;
}
}
// 处理最后一行
for(int j = m - 2; j >=0; --j) {
if(obstacleGrid[n - 1][j] == 1 || dp[n - 1][j + 1] == 0) {
dp[n - 1][j] = 0;
} else {
dp[n - 1][j] = 1;
}
}
for(int i = n - 2; i >= 0; --i) {
for(int j = m - 2; j >= 0; --j) {
// 如果当前格子是障碍物
if(obstacleGrid[i][j] == 1) {
dp[i][j] = 0;
// 路径总数来自于下方(dp[i+1][j])和右方(dp[i][j+1])
} else {
dp[i][j] = dp[i + 1][j] + dp[i][j + 1];
}
}
}
return dp[0][0];
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
④ 动态规划+空间优化
- 对于动态规划的两种解法,都是只需要上一层的解,而不需要上上一层的:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
- 1
- 也就是求第 i 行时,只需要 i-1 行已求解过的值,不需要 i-2行 ,因此可以用滚动数组进行优化,将二维数组改为一维数组(一维数组的大小为列的长度)。
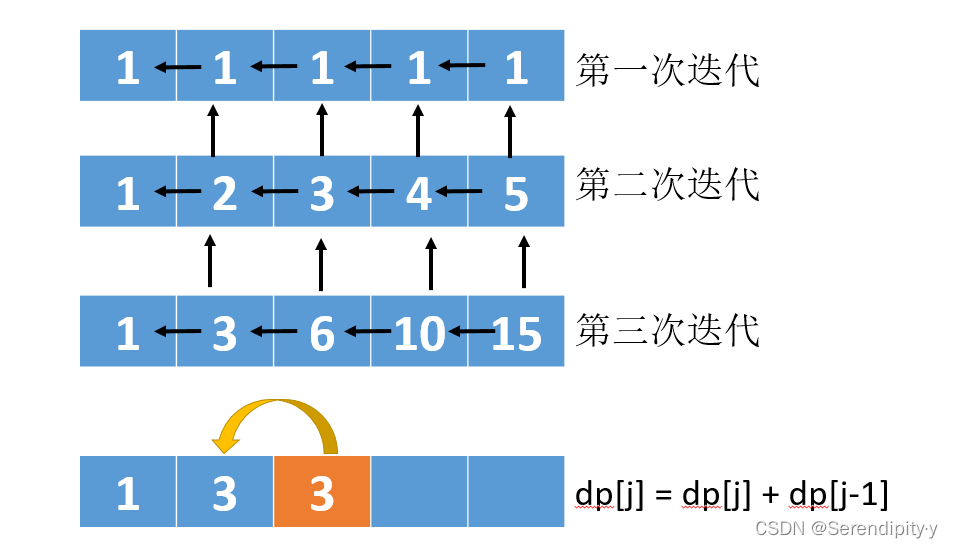
- 第三次迭代时,求第三个格子 6 时,由于左边的值已经是已知的,第二次迭代时同位置的值也是已知的,因此当前值的计算方式就是:
计算当前值 = 以求出的左边值 + 上一次迭代同位置的值
dp[j] = dp[j - 1] + dp[j]
- 1
- 2
- Java 示例:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int n = obstacleGrid.length;
int m = obstacleGrid[0].length;
int[] dp = new int[m];
// 起点可能有障碍物
dp[0] = (obstacleGrid[0][0] == 1) ? 0 : 1;
for(int i = 0; i < n; ++i) {
for(int j = 0; j < m; ++j) {
// 有障碍物的格子直接赋0
if(obstacleGrid[i][j] == 1) {
dp[j] = 0;
}
// 否则dp[j]的值由左方和上一次迭代的dp[j]累加而来
else if(obstacleGrid[i][j] == 0 && j - 1 >= 0) {
dp[j] = dp[j] + dp[j - 1];
}
}
}
return dp[m - 1];
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
文章来源: blog.csdn.net,作者:Serendipity·y,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/Forever_wj/article/details/122848216
【版权声明】本文为华为云社区用户转载文章,如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者



评论(0)