【python】 深入理解递归思想

一、递归定义

递归就是子程序（或函数）直接调用自己或通过一系列调用语句间接调用自己，是一种描述问题和解决问题的基本方法。递归常用来解决结构相似的问题。所谓结构相似，是指构成原问题的子问题与原问题在结构上相似，可以用类似的方法解决。具体地，整个问题的解决，可以分为两部分：第一部分是一些特殊情况，有直接的解法；第二部分与原问题相似，但比原问题的规模小，并且依赖第一部分的结果。实际上，递归是把一个不能或不好解决的大问题转化成一个或几个小问题，再把这些小问题进一步分解成更小的小问题，直至每个小问题都可以直接解决。

基本要素:
基线条件：确定递归到何时终止，函数不再调用自己，也称为递归出口；
递归条件：函数调用自己，将大问题分解为类似的小问题，也称为递归体。

核心思想:
每一次递归，整体问题都要比原来减小，并且递归到一定层次时，要能直接给出结果。

def foo(n):
    if n = 1:
        return 1
    return  foo(n-1)

上面就实现了一个简单的递归函数。
同时需要注意:使用递归函数需要注意防止栈溢出。在计算机中，函数调用是通过栈（stack）这种数据结构实现的，每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。由于栈的大小不是无限的，所以，递归调用的次数过多，会导致栈溢出。会报错：`RecursionError: maximum recursion depth exceeded in comparison

二、递归思想 

  递归算法常用来解决结构相似的问题。
  所谓结构相似，是指构成原问题的子问题与原问题在结构上相似，可以用类似的方法解决。具体地，整个问题的解决，可以分为两部分：第一部分是一些特殊情况，有直接的解法；第二部分与原问题相似，但比原问题的规模小，并且依赖第一部分的结果。 

  本质上，递归是把一个不能或不好解决的大问题转化成一个或几个小问题，再把这些小问题进一步分解成更小的问题，直至每个小问题都可以直接解决。 
  实际上，递归会将前面所有调用的函数暂时挂起，直到递归终止条件给出明确的结果后，才会将所有挂起的内容进行反向计算。其实，递归也可以看作是一种反向计算的过程，前面调用递归的过程只是将表达式罗列出来，待终止条件出现后，才依次从后向前倒序计算前面挂起的内容，最后将所有的结果一起返回。

三、构建函数

基线条件(base case)：
递归程序的最底层位置，在此位置时没有必要再进行操作，可以直接返回一个结果；
所有递归程序都必须至少拥有一个基线条件，而且必须确保它们最终会达到某个基线条件；否则，程序将永远运行下去，直到程序缺少内存或者栈空间；

基本结构
至少一个基线条件：通常在递归函数的开始位置，就设置基线条件；
一系列的规则：使得每次调用递归函数，都趋近于直至达到基线条件。

思想：
1.找到当前这个值与上一个值的关系
2.找到程序的出口 有个明确的结束条件
3.假设当前功能已经完成 每次进入更深一层递归时，问题规模相比上次递归都应有所减少

递归思路：
（1）找重复：看哪一部分是 实现函数的变化；每次进入更深一层递归时，问题规模相比上次递归都应有所减少
（2）找变化：变化的量应该作为参数
（3）找边界（出口）：终止条件

递归可以分为：
（1）直接量+小规模子问题
（2）多个小规模子问题
（3） “切蛋糕”思维
（4）找递推公式，等价交换公式

四、递归剖析

首先“递归”包括两个过程：递“去”的过程，“归”回的过程！先从一个简单的递归函数讲起

def digui(n):
    print(n, '<===1===>')
    if n>0:
        digui(n-1)
    print(n, '<===2===>')
digui(5)
# 5 <===1===>
# 4 <===1===>
# 3 <===1===>
# 2 <===1===>
# 1 <===1===>
# 0 <===1===>
# 0 <===2===>
# 1 <===2===>
# 2 <===2===>
# 3 <===2===>
# 4 <===2===>
# 5 <===2===>

 重点来理解下，首先是一，看上面的列子，例子中没有return，但是不断的调用后，最终还是停止了，因为最后n=0时，di_gi(0)还是去调用，从上往下执行时，遇到if n>0 它被终止了，走不下去了，表明，自己能到达的这层空间已经全部执行完毕；接下来请原地返回吧，返回到哪里？返回到函数的调用者，好我们返回到 di_gui(0)，把“到内部调用函数” 以下的代码全部执行完；执行完，看代码走到末尾，以为走出了最外层函数？注意了，此时它所处的空间并不是最外层哦，因为之前它被调用就在空间里面，所以回到的是 di_gui(1)的这一层空间，现在才是真正的开始“回”，所以继续把di_gui(1)的这一层空间，“到内部调用函数”以下的代码全部执行完，回到di_gui(2)的这一层空间…直到到达最开始 从外部调用，让参数5进入的最外层空间位置，才走出来！

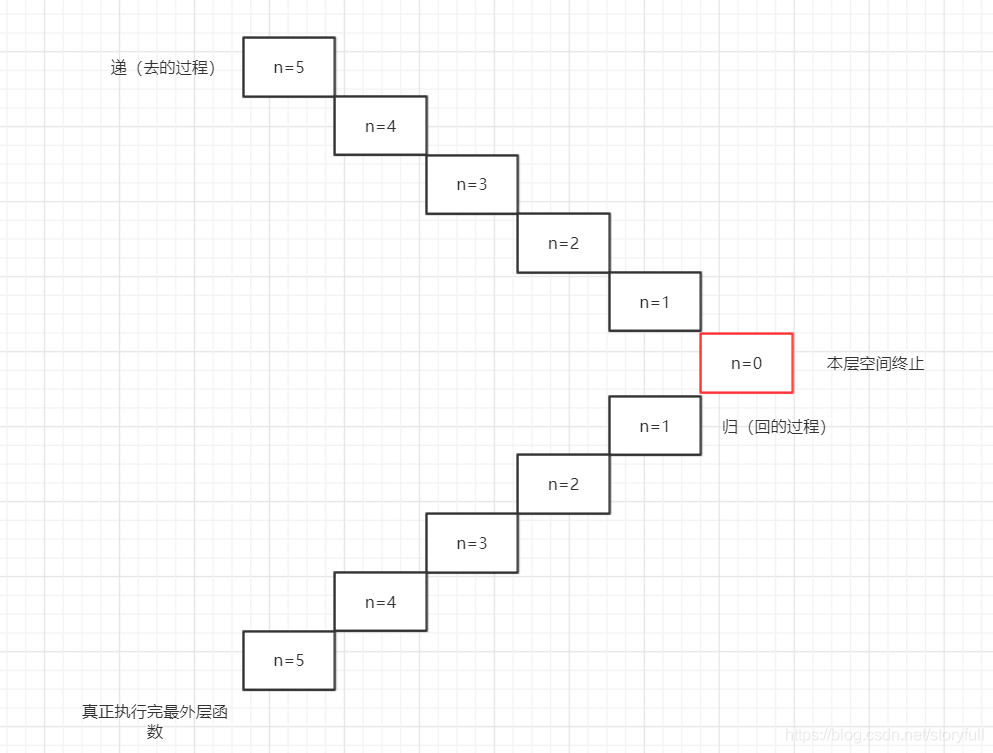
 从内存角度（本质）来分析：每调用一次函数，都会单独开辟一份栈帧空间，递归函数就是不停的开辟和释放栈帧空间的过程，具体来理解下：一个普通函数从执行到结束，就是一个开辟空间和释放空间的过程；而递归函数是在调用最外层函数时，先开辟一个最外层空间，每调用一次自身，就会在最外层空间内，再自己开辟本次的空间（所以递归耗内存）（还有一种说法是，不断的本次空间的基础上再开辟空间，等于是不断的嵌套，其实这两种说法本质上是一样的，因为信息都可以做到不共享），空间之间如果不通过参数传递或者用return 返回值，信息是不共享的

递归的执行过程：首先，递归会执行“去”的过程，只需要满足终止条件，就会一直在函数内，带着更新的参数，调用函数自身，注意：到内部调用函数， 以下面的代码不会被执行，而是暂停阻塞；此时 随着函数每调用一次自身，还没有触发 返回值和到达终止条件，等同于在原来的基础上不断“向下/向内”开辟新的内存空间，记住，每次调用一次函数，就不是处在同一空间

去的过程：就是不断的开辟空间，在回的过程，不停的释放空间，递归函数就是不停的开辟和释放空间的过程
回的过程：最后一层空间所有代码执行完毕，就会触发回的过程，或者遇到return也会触发回的过程，回到上一层函数调用的位置

“递”去的过程结束有两种情况 一是：当前这层空间函数全部执行结束（终止条件），二是：执行到了return 返回值，直接返回； 
每一层递归空间都是独立的个体，独立的副本，资源不共享

五、尾递归优化

1. 在计算机中，函数调用是通过栈(stack)这种数据结构实现的，每当进入一个函数调用，栈就会加一层栈帧，每当函数返回，栈就会减一层栈帧。由于栈的大小不是无限的，所以，递归调用的次数过多时，可能会导致栈溢出；

2. 尾递归：指函数返回时调用自身本身，并且return语句不能包含表达式。这样，编译器或者解释器就可以把尾递归做优化，使递归本身无论调用多少次，都只占用一个栈帧，不会出现栈溢出的情况；

3. 尾递归和循环的效果是一样的，实际上，可以把循环看成是一种特殊的尾递归函数；

4. 尾递归是优化递归防止溢出的一种方法，但并不能彻底解决溢出。举个形象的例子：开车减速慢行可以少出车祸，但减速慢行不一定不出车祸；

5. 阶乘的fact(n)函数，return语句，返回了n * fact(n - 1)的乘法表达式，不是尾递归。要改成尾递归方式，需要把每一步的乘积传入到递归函数中。

• 参考代码如下：

def factorial(n):
    return fact_iter(n, 1)

def fact_iter(n, product):
    if n == 1:
        return product
    return fact_iter(n - 1, n * product)

print(factorial(5))
120

• 将每次的乘积，存入到 product 中，return fact_iter(n-1, n * product) 返回的仅仅是函数本身，n - 1 和 n * product 在函数调用前就会被计算出来，不影响函数调用；

• 优化的实质，就是将原本倒序的计算，通过 n * product 变为了正序的计算，还是递归的思想，但是不会占用其他的栈帧，因为所有的结果都已近存放在了 product 中。fact(5)对应的fact_iter(5, 1)的调用如下：

  ===> fact_iter(5, 1)
  ===> fact_iter(4, 5)
  ===> fact_iter(3, 20)
  ===> fact_iter(2, 60)
  ===> fact_iter(1, 120)
  ===> 120
  

• 尾递归调用时，如果做了优化，栈不会增长，无论多少次调用也不会导致栈溢出。

• 遗憾的是，大多数编程语言没有针对尾递归做优化，Python解释器也没有做优化，任何递归函数都存在栈溢出的问题。所以，即使把上面的fact(n)函数改成尾递归方式，也可能导致栈溢出。

六.递归实例

斐波拉契数列

• 数列：规定F(0) = 0，F(1) = 1，从第三项起，每一项都等于前两项的和，即F(N) = F(N - 1) + F(N - 2) (N >= 2)
• 参考代码

def fibonacci(n):
    if n < 2:
        return n 
    return fibonacci(n-1) + fibonacci(n-2)

print(fibonacci(10))
55

n项指定值之和

• s = a * 1 + a * 2 + a * 3 + a * 4 + ...... + a * n，SSS(a, n) = SSS(a, n-1) + a * n
• 参考代码

def n_sum(a, n):
    if n == 1:
        return a
    return n_sum(a, n - 1) + n * a 

print(n_sum(2, 5))
30

快速排序

• 原理：基于分治策略，设定一个基准线(pivot)，将数据与基准线对比，分成大于和小于两部分，通过递归，不断分治实现数据的排序；
• 参考代码

def quick_sort(n):
    if len(n) < 2:
        return n 
    else:
        pivot = n[0]
        left = [x for x in n[1:] if x < pivot]
        right = [x for x in n[1:] if x > pivot]
    return quick_sort(left) + [x for x in n if x == n[0]] + quick_sort(right)

print(quick_sort([5,11,3,5,8,2,6,7,3]))
[2, 3, 3, 5, 5, 6, 7, 8, 11]

汉诺塔问题

• 把问题理解为三步：第一步，将n-1个塔从A移动到B（中间使用到了C）；第二步，将第n个塔从A移动到C；第三步，将n-1个塔从B移动到C（中间用到了A）
• 参考代码

N = 0
def hannoi(n,a,b,c):
    global N
    if n>0:
        hannoi(n-1, a, c, b)
        N = N + 1
        print('第{}次移动： move from {} to {}'.format(N, a, c))
        hannoi(n-1, b, a, c)

五、递归应用

递归算法一般用于解决三类问题
数据的定义是按递归定义的，比如：Fibonacci函数、阶乘等；
问题的解法是按递归算法实现的，比如：回溯法；
数据的结构形式是按递归定义的，比如：树的遍历、图的搜索等；

优点
递归使代码看起来更加整洁、优雅；
递归可以将复杂任务分解成更简单的子问题；
使用递归比使用一些嵌套迭代更容易解决问题。

缺点
递归的逻辑很难调试、跟进；
递归的运行效率较低。因为在递归的调用过程中，系统会为每一层的返回值或局部变量开辟新的栈进行存储。递归次数过多容易造成栈溢出。