今日头条笔试2017年4月18日 A题 查找元素?
目录
2017年4月18日 A题 查找元素?
题目:

我的代码(测试用例100%通过):
-
#include <iostream>
-
#include<algorithm>
-
using namespace std;
-
-
int l[100000], m;
-
-
bool find(int k)
-
{
-
int low = 0, high = m - 1, mid;
-
while (low < high - 1)
-
{
-
mid = (low + high) / 2;
-
if (l[mid] == k)return true;
-
if (l[mid] > k)high = mid;
-
else low = mid;
-
}
-
if (l[low] == k || l[high] == k)return true;
-
return false;
-
}
-
-
int main()
-
{
-
int n, k;
-
scanf("%d", &m);
-
for (int i = 0; i < m; i++)scanf("%d", &l[i]);
-
sort(l, l + m);
-
scanf("%d", &n);
-
while (n--)
-
{
-
scanf("%d", &k);
-
if (find(k))printf("%d ", k);
-
}
-
return 0;
-
}
2017年4月18日 B题 DAU 统计
题目描述:
日活跃用户数 (DAU) 是衡量一个产品表现的重要指标。
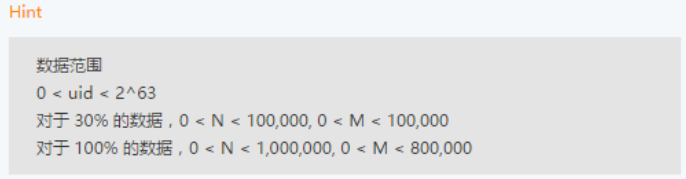
需要编写程序,根据给定的某一天的 N 条访问记录,对当天的用户总数 M 进行统计。
每个用户可能访问多次。
为了方便,我们用数字 (uid) 唯一标识每个用户。
input
每一行包含一个 uid,遇到 0 时认为输入结束。
输入共包含 N+1 行,可认为是无序的。
output
一个数字:去重后 uid 的数量 M。
样例输入
12933
111111
59220
69433
59220
111111
0
样例输出
4
我的代码(测试用例100%通过):
-
#include <iostream>
-
#include<set>
-
using namespace std;
-
-
int main()
-
{
-
set<long long>se;
-
se.clear();
-
long long uid;
-
int M;
-
while (scanf("%lld", &uid))
-
{
-
if (uid == 0)break;
-
se.insert(uid);
-
}
-
cout << se.size();
-
return 0;
-
}
这个题目用set非常简单,而且效率也很高,因为set的插入(查找)是log的时间
2017年4月18日 C题 形式化算式
题目描述:
我们有如下形式化的数字
* *** *** * * *** *** *** *** *** ***
* * * * * * * * * * * * * *
* *** *** *** *** *** * *** *** * *
* * * * * * * * * * * * *
* *** *** * *** *** * *** *** ***
(* 下附图片供参考)
分别表示 1 2 3 4 5 6 7 8 9 0
有如下形式化的符号:
* * * * ****
*** *** * *
* * * * **** **
**
(* 下附图片供参考)
分别表示 + - * / = 小数点
输入
现在 将输入一个算式
输出
你要将该算式计算之后按照上述形式化的方式输出
各个数字和符号之间空两格
无法整除则保留两位小数
样例输入
10 + 31
样例输出
* *** *** * * * *
* * * * * * **** * * *
* * * *** *** * *** *
* * * * * * **** * *
* *** *** * * *
(* 下附图片供参考)
Hint
样例输入2:
2 / 5
样例输出2:
*** *** *** * *
* * * **** * * * *
*** * *** * * ***
* * * **** * * ** *
*** *** *** ** *
(* 下附图片供参考)
数据范围:
20%的数据 输入的数字和运算结果都是个位数
100%的数据保证 输入数字和答案都小于10000
100%的数据保证 输入数字不会出现小数
80%的数据保证 运算结果不会出现小数
我的代码(测试用例80%通过):
-
#include <iostream>
-
#include<string.h>
-
using namespace std;
-
-
char ans[5][100], char0 = '0';
-
const char cs[17] = "1234567890+-*/.=";
-
const char s[5][100] = {
-
"* *** *** * * *** *** *** *** *** *** ",
-
"* * * * * * * * * * * * * * * * * * **** ",
-
"* *** *** *** *** *** * *** *** * * *** *** * * ",
-
"* * * * * * * * * * * * * * * * * ** **** ",
-
"* *** *** * *** *** * *** *** *** ** "
-
};
-
-
void add(char c)
-
{
-
int k = -1, num = 5;
-
for (int i = 0; i < 16; i++)if (cs[i] == c)k = i;
-
if (k == -1)return;
-
if (k == 15)num = 6;
-
if (k == 0)num = 3;
-
if (k == 14)num = 4;
-
for (int i = 0; i < 5; i++)strncat(ans[i], s[i] + k * 5, num);
-
}
-
-
void add(int n)
-
{
-
if (n >= 10)
-
{
-
add(n / 10);
-
add(n % 10);
-
return;
-
}
-
add(char(char0 + n));
-
}
-
-
void add(double x)
-
{
-
int n = int(x);
-
double eps = 0.0000001, r = x - n;
-
if (n - x < eps && x - n < eps)r = 0;
-
add(n);
-
if (r == 0)return;
-
add('.');
-
n = int(r * 100);
-
if (n % 10 == 0)n /= 10;
-
add(n);
-
}
-
int main()
-
{
-
for (int i = 0; i < 5; i++)ans[i][0] = '\0';
-
int a, b, r1;
-
double r2 = -1;
-
char ch = ' ';
-
scanf("%d %c %d", &a, &ch, &b);
-
add(a);
-
add(ch);
-
add(b);
-
add('=');
-
if (ch == '+')r1 = a + b;
-
if (ch == '-')r1 = a - b;
-
if (ch == '*')r1 = a*b;
-
if (ch == '/')r2 = a*1.0 / b;
-
if (r2 == -1)add(r1);
-
else add(r2);
-
for (int i = 0; i < 5; i++)cout << ans[i] << endl;
-
return 0;
-
}
这个代码我觉得写得还是不错的,就是不知道为什么只通过了80%,应该是void add(double x)函数里面有问题,小数部分处理的还不到位。
首先,把所有字符存到cs里面,把对应的形式化符号全部存到s里面,编程起来方便很多。
其次,对add重载了3次,而且互相调用,也使得编程简单了很多。
2017年4月18日 D题 任务执行策略
题目描述:
我们有一批任务在 mesos 当中。这批任务要么不依赖其它任务,要么一定恰好依赖于两个任务,并且整个依赖关系会构成一个三角模型:
Job(1, 1)
Job(2, 1) Job(2, 2)
Job(3, 1) Job(3, 2) Job(3, 3)
……
Job(n, 1) Job(n, 2) …… Job(n, n)
如上图,Job(1, 1) 依赖于 Job(2, 1) 和 Job(2, 2);Job(2, 2) 依赖于 Job(3, 2) 和 Job(3, 3);对于任意 1 <= i < n, 1 <= j <= n,Job(i, j) 依赖于 Job(i + 1, j) 和 Job(i + 1, j + 1)。最后一行的任务没有任务依赖。
这批任务有一个特点,每个任务都需要配合它所依赖的任务来执行。也就是说,一个任务某次运行是有效的,当且仅当至少满足下列一个条件:
1. 该任务不依赖其它任务;
2. 该任务依赖的两个任务都是有效的。
每个任务都预先设定了一个权重 weight(i, j)。现在由于资源上的限制,我们只能挑选其中的 k 个任务来运行。我们希望所有被运行的任务都是有效的,并使得所有运行过的任务的权重之和最大。
输入
第一行是两个整数 n 和 k。
接下来 n 行,其中第 i 行 (1 <= i <= n) 包含 i 个整数,给出各个任务的权重。这个三角形也同时描述了任务的依赖关系。
输出
输出仅包含一个整数,即所求的最大权重和。
样例输入
3 4
1
2 3
1 1 1
样例输出
6
Hint
对于 30% 的数据,1 <= n, k <= 50;
对于 100% 的数据,1 <= n <= 100,1 <= m <= C(n + 1, 2),1 <= weight(i, j) <= 1000。
这个题目有点像线段树,又有点像动态规划,反正我还没开始写就结束了。因为没法提交了所以也不想写了。
答案是动态规划。
下面是今日头条的公众号里面公布的答案:
动态规划。
如图,如果我们选择了 Job(i, j),除了要同时选中 Job(i + 1, j)之外,也意味着 Job(i + 1, j + 1), Job(i + 2, j + 2) … Job(i + d, j + d) 这一条链全部都要选中。既然每条斜线都是选择一个后缀,因此可以据此划分阶段进行动态规划。
考虑 f[i, j, m] 表示前 i 条斜线,总共选择了 m 个任务,其中第 i 条斜线自下往上选择了 j 个任务时的最大权值和,那么转移时只需要保证第 i - 1 条斜线需要选择的任务个数 >= j - 1 即可。状态转移方程为
f[i, j, m] = max(f[i - 1, j2, m - j]) + sum[i, j] (j - 1 <= j2 <= i)
这里 sum[i, j] 表示第 i 条斜线的最下面 j 个任务的权值之和。这个转移的复杂度是 O(n) 的,总复杂度会达到 O(n^3 * m),不符合要求。问题的关键在于如何快速地获得 max(f[i - 1, j2, m - j]) 这一项,这里的优化方式很多,简单举两个方法:
1. 用另一个数组维护每条斜线的 f 数组的后缀的最大值,那么 max(f[i - 1, j2, m - j]) 这一项就可以 O(1) 得到;
2. 将 f 的定义改为,第 i 条斜线自下往上 至少 选择了 j 个任务的最大权值和,那么转移时就不需要枚举 j2 了。具体的转移方程留给各位重新推导一下。
优化之后可以得到 O(n^2 * m) 的时间复杂度。
当然这个题目也可以有另外的状态划分方式。注意到 Job(i, j) 选中时,除了 Job(i + 1, j + 1) 这个任务之外,Job(i + 1, j), Job(i + 2, j) … Job(n, j) 这一条链也必须选中,那么也可以用和上述对称的方式来构造转移方程。时间复杂度同样也是 O(n^2 * m) 的。
2017笔试题?

上面的代码的来源我不清楚,可能是官方给的。
下面说下我的解决方案。
首先化简方程:x+y-x|y=0
这个方程的左边可以化简为x&y
所以方程即x&y=0
现在问题转化成:求满足x&y=0的第k小的正整数。
我的代码:
-
#include<iostream>
-
using namespace std;
-
-
int main()
-
{
-
int x, k, y, t;
-
while (cin >> x >> k)
-
{
-
t = 1, y = 0;
-
while (k)
-
{
-
if (x % 2 == 0)y += t*(k % 2), k /= 2;
-
x /= 2, t *= 2;
-
}
-
cout << y << endl;
-
}
-
return 0;
-
}
文章来源: blog.csdn.net,作者:csuzhucong,版权归原作者所有,如需转载,请联系作者。
原文链接:blog.csdn.net/nameofcsdn/article/details/112210335
- 点赞
- 收藏
- 关注作者


评论(0)