目录

一，卢卡斯定理

二，OJ实战

FZU - 2020 组合

一，卢卡斯定理

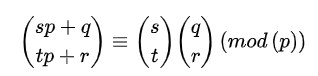
其中 0<= q,r <p

二，OJ实战

FZU - 2020 组合

题目：

Description

给出组合数C(n,m), 表示从n个元素中选出m个元素的方案数。例如C(5,2) = 10, C(4,2) = 6.可是当n,m比较大的时候，C(n,m)很大！于是xiaobo希望你输出 C(n,m) mod p的值！
Input

输入数据第一行是一个正整数T,表示数据组数 (T <= 100) 接下来是T组数据，每组数据有3个正整数 n, m, p (1 <= m <= n <= 10^9, m <= 10^4, m < p < 10^9, p是素数)
Output

对于每组数据，输出一个正整数，表示C(n,m) mod p的结果。
Sample Input

2
5 2 3
5 2 61
Sample Output

1
10

因为给出了T的上限100，m的上限10000，所以不需要数组，每次直接算出结果即可。

计算的时候需要用到逆元，这应该是必须用到的。

代码：

  

   

    

     

    
    

     

      #include<iostream>
     
    
   

    

     

    
    

     

      using namespace std;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int p;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      long long get_mi(int n, int k)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	if (k == 0)return 1;
     
    
   

    

     

    
    

     
	long long r = get_mi(n, k / 2) % p;
     
    
   

    

     

    
    

     

      	r = (r*r) % p;
     
    
   

    

     

    
    

     
	if (k % 2)r = (r*n) % p;
     
    
   

    

     

    
    

     
	return r;
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int main()
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	int t, n, m;
     
    
   

    

     

    
    

     

      	cin >> t;
     
    
   

    

     

    
    

     
	while (t--)
     
    
   

    

     

    
    

     

      	{
     
    
   

    

     

    
    

     

      		cin >> n >> m >> p;
     
    
   

    

     

    
    

     
		long long r = 1;
     
    
   

    

     

    
    

     
		for (int i = 1; i <= m; i++)r = (r*(n - i + 1) % p)*get_mi(i, p - 2) % p;
     
    
   

    

     

    
    

     

      		cout << r << endl;
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
	return 0;
     
    
   

    

     

    
    

     

      }
     
    
  
 

结果AC了，不过不快，703ms

用快速幂求逆元自然是必须用到的，上述的代码只用了这个。

如果再用上卢卡斯定理，肯定会快一些，快多少就不好说了，要看给的数据是什么情况。

代码：

  

   

    

     

    
    

     

      #include<iostream>
     
    
   

    

     

    
    

     

      using namespace std;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int p;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      long long get_mi(int n, int k)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	if (k == 0)return 1;
     
    
   

    

     

    
    

     
	long long r = get_mi(n, k / 2) % p;
     
    
   

    

     

    
    

     

      	r = (r*r) % p;
     
    
   

    

     

    
    

     
	if (k % 2)r = (r*n) % p;
     
    
   

    

     

    
    

     
	return r;
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int f(int n, int m)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	long long r = 1;
     
    
   

    

     

    
    

     
	if (n > p)r = f(n / p, m / p)*f(n%p, m%p) % p;
     
    
   

    

     

    
    

     
	else for (int i = 1; i <= m; i++)r = (r*(n - i + 1) % p)*get_mi(i, p - 2) % p;
     
    
   

    

     

    
    

     
	return r;
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int main()
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	int t, n, m;
     
    
   

    

     

    
    

     
	scanf("%d", &t);
     
    
   

    

     

    
    

     
	while (t--)
     
    
   

    

     

    
    

     

      	{
     
    
   

    

     

    
    

     
		scanf("%d%d%d", &n, &m, &p);
     
    
   

    

     

    
    

     
		printf("%d\n", f(n, m));
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
	return 0;
     
    
   

    

     

    
    

     

      }
     
    
  
 

然而结果还是703ms，数据体现不出这个算法的威力。

文章来源: blog.csdn.net，作者：csuzhucong，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/nameofcsdn/article/details/115764969