目录

一，容斥原理

二，OJ实战

CSU 2140: Rikka's function

CSU 1803: 2016

UVA - 10325 The Lottery

一，容斥原理

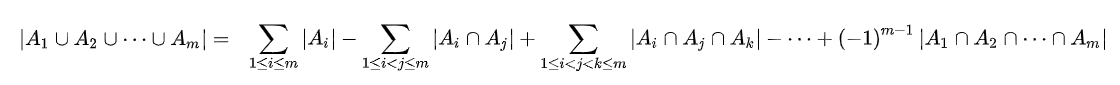
二，OJ实战

CSU 2140: Rikka's function

题目：

思路：

代码：

  

   

    

     

    
    

     

      #include<iostream>
     
    
   

    

     

    
    

     

      using namespace std;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int p = 1000000007;
     
    
   

    

     

    
    

     

      long long f[1000005];
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      long long get_mi(long long n, int k)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	if (k == 0)return 1;
     
    
   

    

     

    
    

     
	long long r = get_mi(n, k / 2) % p;
     
    
   

    

     

    
    

     

      	r = (r*r) % p;
     
    
   

    

     

    
    

     
	if (k % 2)r = (r*n) % p;
     
    
   

    

     

    
    

     
	return r;
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int main()
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	int n, m;
     
    
   

    

     

    
    

     

      	cin >> n >> m;
     
    
   

    

     

    
    

     

      	f[m] = m, f[m + 1] = 1;
     
    
   

    

     

    
    

     
	for (int i = m - 1; i >= 1; i--)f[i] = f[i + 1] * i%p;
     
    
   

    

     

    
    

     
	long long s = 0, t = get_mi(f[1], p - 2) % p;
     
    
   

    

     

    
    

     
	for (int i = 0; i <= m; i++)
     
    
   

    

     

    
    

     

      	{
     
    
   

    

     

    
    

     
		long long r = t;
     
    
   

    

     

    
    

     
		if (i % 2)r *= -1;
     
    
   

    

     

    
    

     

      		r = r*f[i+1] % p;
     
    
   

    

     

    
    

     

      		r = r*f[m-i+1] % p;
     
    
   

    

     

    
    

     

      		r = r*get_mi(m - i, n) % p;
     
    
   

    

     

    
    

     

      		s += r;
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     

      	s = s%p + p;
     
    
   

    

     

    
    

     

      	cout << s%p << endl;
     
    
   

    

     

    
    

     
	return 0;
     
    
   

    

     

    
    

     

      }
     
    
  
 

CSU 1803: 2016

题目：

Description

 给出正整数 n 和 m，统计满足以下条件的正整数对 (a,b) 的数量：
1. 1≤a≤n,1≤b≤m;
2. a×b 是 2016 的倍数。
Input

输入包含不超过 30 组数据。
每组数据包含两个整数 n,m (1≤n,m≤10 9).
Output
对于每组数据，输出一个整数表示满足条件的数量。
Sample Input
32 63
2016 2016
1000000000 1000000000
Sample Output
1
30576
7523146895502644

这个题目直接枚举g=gcd(a,2016)即可
2016=2*2*2*2*2*3*3*7，所以g有6*3*2=36种情况。

对于每个g,求a满足gcd(a,2016)恰好是g，求b使得2016| a*b

一，求a满足gcd(a,2016)恰好是g

即求1,2,3......n/g这些数中，有多少个和2016/g互质，用容斥原理即可

二，求b使得2016| a*b

即求1,2,3......m这些数中，有多少个是2016/g的倍数，答案就是m*g/2016

代码：
 

  

   

    

     

    
    

     

      #include<iostream>
     
    
   

    

     

    
    

     

      using namespace std;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int n, m;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      long long f(int g)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	int nn = n / g;
     
    
   

    

     

    
    

     
	long long s = nn - (1008 % g == 0)*nn / 2 - (672 % g == 0)*nn / 3 - (288 % g == 0)*nn / 7;
     
    
   

    

     

    
    

     

      	s += (336 % g == 0)*nn / 6 + (96 % g == 0)*nn / 21 + (144 % g == 0)*nn / 14 - (48 % g == 0)*nn / 42;
     
    
   

    

     

    
    

     
	long long gg = g;
     
    
   

    

     

    
    

     
	return gg*m / 2016 * s;
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      long long f7(int g)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	return f(g) + f(g * 7);
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      long long f5(int g)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	return f7(g) + f7(g * 3) + f7(g * 9);
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int main()
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	while (cin >> n >> m)cout << f5(1) + f5(2) + f5(4) + f5(8) + f5(16) + f5(32) << endl;
     
    
   

    

     

    
    

     
	return 0;
     
    
   

    

     

    
    

     

      }
     
    
  
 

UVA - 10325 The Lottery

题目：

用了状态压缩来枚举2^m种状态，用k对应状态。

注意一个细节，当r超过n时，r/n就已经是0了，就不要再继续求lcm了，否则会越界，因为多个数的lcm很容易超过long long的范围。

代码：

  

   

    

     

    
    

     

      #include<iostream>
     
    
   

    

     

    
    

     

      using namespace std;
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int gcd(int a, int b)
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	if (b)return gcd(b, a%b);
     
    
   

    

     

    
    

     
	return a;
     
    
   

    

     

    
    

     

      }
     
    
   

    

     

    
    

     
 
     
    
   

    

     

    
    

     

      int main()
     
    
   

    

     

    
    

     

      {
     
    
   

    

     

    
    

     
	int n, m, l[15], s;
     
    
   

    

     

    
    

     
	while (cin >> n >> m)
     
    
   

    

     

    
    

     

      	{
     
    
   

    

     

    
    

     

      		s = 0;
     
    
   

    

     

    
    

     
		for (int i = 0; i < m; i++)cin >> l[i];
     
    
   

    

     

    
    

     
		for (int k = 0; k < (1 << m); k++)
     
    
   

    

     

    
    

     

      		{
     
    
   

    

     

    
    

     
			long long r = 1, b = 0;
     
    
   

    

     

    
    

     
			for (int i = 0; i < m; i++)if (k&(1 << i))
     
    
   

    

     

    
    

     

      			{
     
    
   

    

     

    
    

     
				if (r <= n)r *= l[i] / gcd(l[i], r);
     
    
   

    

     

    
    

     

      				b++;
     
    
   

    

     

    
    

     

      			}
     
    
   

    

     

    
    

     
			if (b % 2)s -= n/r;
     
    
   

    

     

    
    

     
			else s += n/r;
     
    
   

    

     

    
    

     

      		}
     
    
   

    

     

    
    

     

      		cout << s << endl;
     
    
   

    

     

    
    

     

      	}
     
    
   

    

     

    
    

     
	return 0;
     
    
   

    

     

    
    

     

      }
     
    
  
 

文章来源: blog.csdn.net，作者：csuzhucong，版权归原作者所有，如需转载，请联系作者。

原文链接：blog.csdn.net/nameofcsdn/article/details/115913678