[toc]

算法效率衡量

执行时间反应算法效率

对于同一问题, 我们给出了两种解决算法, 在两种算法的实现中, 我们对程序执行的时间进行了测算, 发现两段程序执行的时间相差悬殊 ( 126.514 秒相比于 0.997 秒), 由此我们可以得出结论: 实现算法程序的执行时间可以反应出算法的效率, 即算法的优劣.

执行结果:

注: 每台机器执行的总时间不同, 但是执行基本运算数量大体相同

单靠时间值绝对可信吗?

假设我们将第二次尝试的算法程序运行在一台配置古老性能低下的计算机中, 情况会如何? 很可能运行时间并不会比我们的电脑中运行算法一的 126.514 秒块多少.

单纯依靠运行时间来比较算法的优劣不一定是客观准确的!

程序的运行离不开计算机环境 ( 包括硬件和操作系统 ), 这些客观原因会影响程序运行的速度并反映在程序的执行时间上. 那么如果才能客观的评判一个算法的优劣呢?

时间复杂度与 "大O记法"

我们假定计算机执行算法每一个基本操作的时间是固定的一个单位, 那么有多少个基本操作就代表会花费多少时间单位. 虽然对于不同的机器环境而言, 确切的单位时间是不同的, 但是对于算法进行多少个基本操作 ( 即花费多少时间单位 ) 在规模数量上是相同的, 由此可以忽略机器环境的影响而客观的反应算法的时间效率.

对于算法的时间效率, 我们可以用 "大O记法" 来表示.

"大O记法": 对于单调的整数函数 f, 如果存在一个整数 g 和常数 C>0, 使得对于充分大的 n 总有 f(n) <= c*g(n), 就是说函数 g 是 f 的一个渐进函数 ( 忽略常数 ), 记为 f(n) = O(g(n)). 也就是说, 在趋向无穷的极限意义下, 函数 f 的增长速度受到函数 g 的约束, 亦即函数 f 与函数 g 的特征相似.

时间复杂度: 假设存在函数 g, 使得算法 A 处理规模为 n 的问题示例所用时间为 T(n) = O(g(n)), 则称 O(g(n)) 为算法 A 的渐近时间复杂度, 简称时间复杂度, 记为 T(n)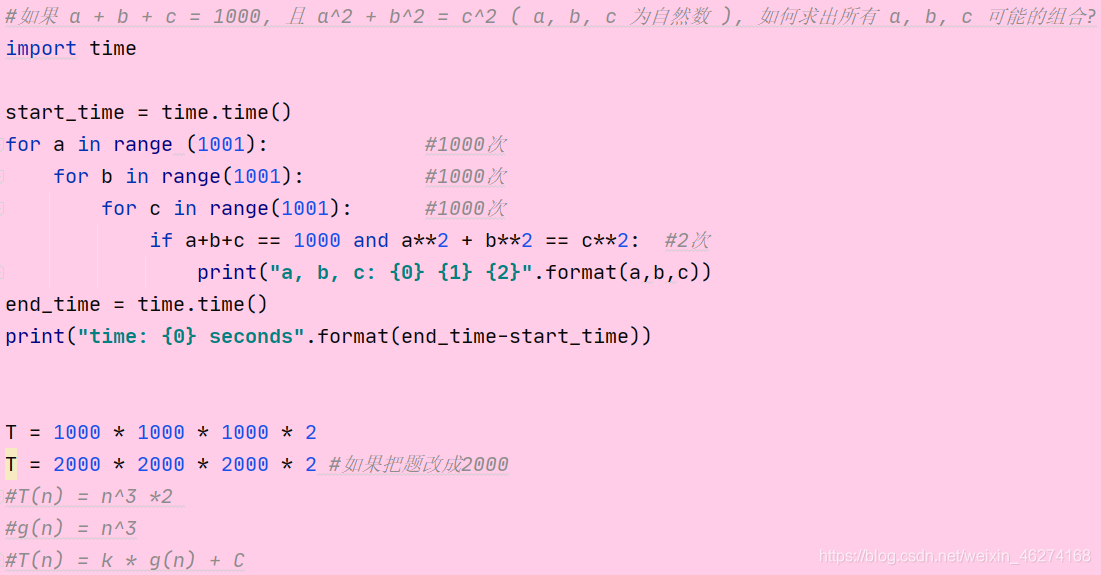

如何理解 "大O记法"

对于算法进行特别具体的细致分析虽然很好, 但在实践中的实际价值有限. 对于算法的时间性质和空间性质, 最重要的是其数量级和趋势, 这些是分析算法效率的主要部分. 而计算量法基本操作数量的规模函数中那些常量因子可以忽略不计. 例如, 可以认为 3n^2 和 100n^2 属于同一个量级, 如果两个算法处理同样规模实例的代价分别为这两个函数, 就认为他们的效率 "差不多", 都为 n^2 级. 

文章来源: iamarookie.blog.csdn.net，作者：我是小白呀，版权归原作者所有，如需转载，请联系作者。

原文链接：iamarookie.blog.csdn.net/article/details/109173131