数据结构系列之二叉树相关概念

数据结构系列之二叉树相关概念

1、什么是二叉树？

二叉树是一种每个节点最多有两个度，也就是说每个节点最多有两个子节点的树，树形结构是数据结构中很常见的，如图是一棵二叉树，其中，5节点是根节点，在其左边的是左节点，右边的是右节点，节点1、3、4、7是叶子节点，也即没有一个节点的节点

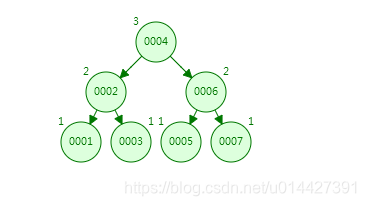
2、二叉树的类型

二叉树可以分为满二叉树、全二叉树、完美二叉树

• 满二叉树
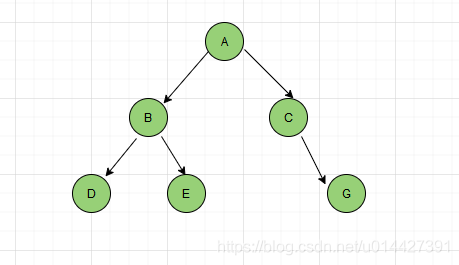
  满二叉树只会有0个子节点（叶子节点）或者2个子节点，不会有1个子节点的情况
  
  如图，这是一棵非满二叉树，因为C节点只有一个节点，不符合满二叉树的特点
  

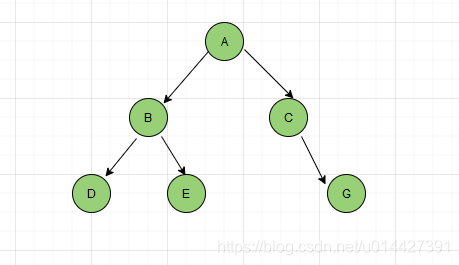
• 全二叉树
  全二叉树是除了最后一个级别之外，其它级别都有两个子节点，如图二叉树虽然不是满二叉树，却符合全二叉树的特点
  

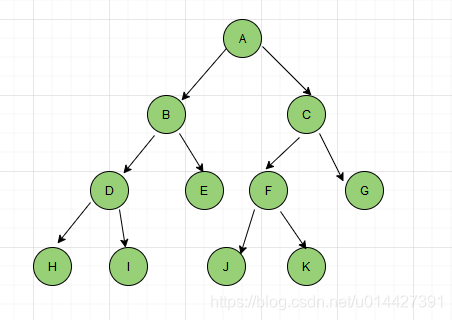
• 完美二叉树
  完美二叉树既是满二叉树，也是全二叉树，完美二叉树除了叶子节点之外的每一个节点都有两个孩子节点
  

3、二叉树遍历

二叉树的搜索规则有：

• 前序遍历：就是先访问根节点，再访问左节点，最后访问右节点，即根-左-右遍历
• 中序遍历：就是先访问左节点，再访问根节点，最后访问右节点，即左-根-右遍历
• 后序遍历：就是先访问左节点，再访问右节点，最后访问根节点。即左-右-根遍历
  
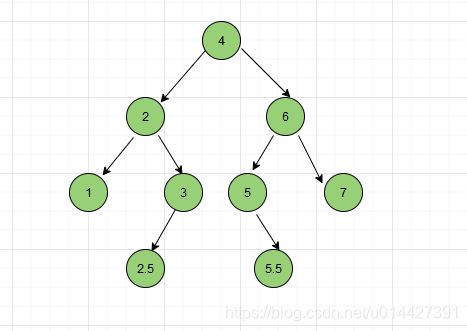
  如上图所示，这里按照前序遍历、中序遍历、后序遍历，进行实践：

前序遍历：4、2、1、3、2.5、6、5、5.5、7
中序遍历：1、2、2.5、3、4、5、5.5、6、7
后序遍历：1、2.5、3、2、5.5、5、7、6、4

4、前驱后继节点

• 前驱节点：前驱节点也即小于当前节点的最大值
• 后继节点：后继节点也即大于当前节点的最小值

查找最小值：沿着某个节点的右节点一路查找，一直往左边找
查找最大值：沿着某个节点的左节点一路查找，一直往右边找

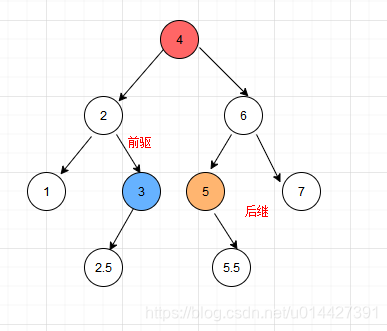
5、删除节点

二叉树的删除分为三种情况：

• ①、是叶子节点，直接删除既可
• ②、只有一个节点，其实查找前驱节点或者后继节点来替代，左节点即前驱节点，右节点即后继节点
• ③、有两个子节点的情况，同样也是寻找前驱节点或者后继节点来替代

综上所述，删除节点的过程其实就是寻找前驱节点或者后继节点来替代

6、查找局限性

一个二叉查找树是由n个节点随机构成，所以会有一些特殊的情况，会出现二叉树退化为n个节点的线性链

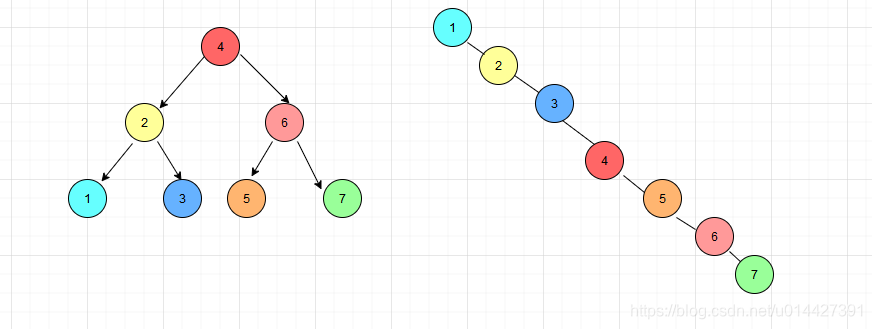
7、平衡查找二叉树（BST）

为了避免上面提到的极端不平衡的情况，就需要有平衡查找二叉树（BST树）

平衡查找二叉树（Balanced Search Tree , BST），有如下的特性：

• 左右子树都是平衡的
• 左右子树的高度最多相差1

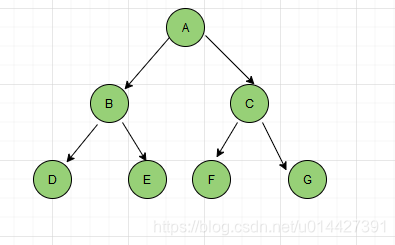
如图就是一颗平衡查找二叉树

平衡查找二叉树两款具有代表性的平衡术分别为AVL树（高度平衡树，具备二叉搜索树的全部特性，而且左右子树高度差不超过1）和红黑树

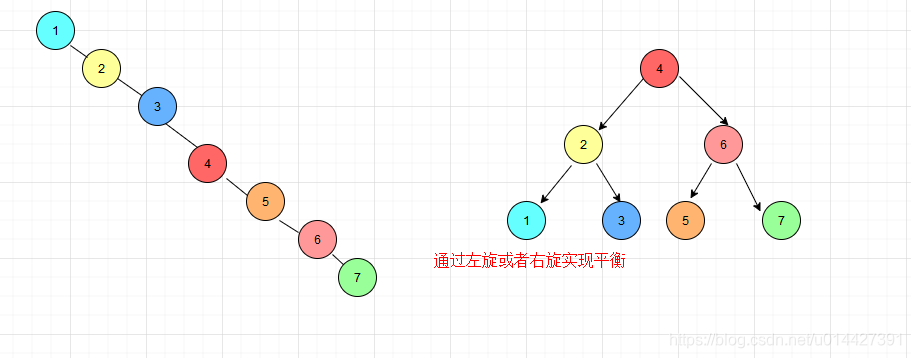
画图表示平衡二叉树的生成过程，每次新增一个节点

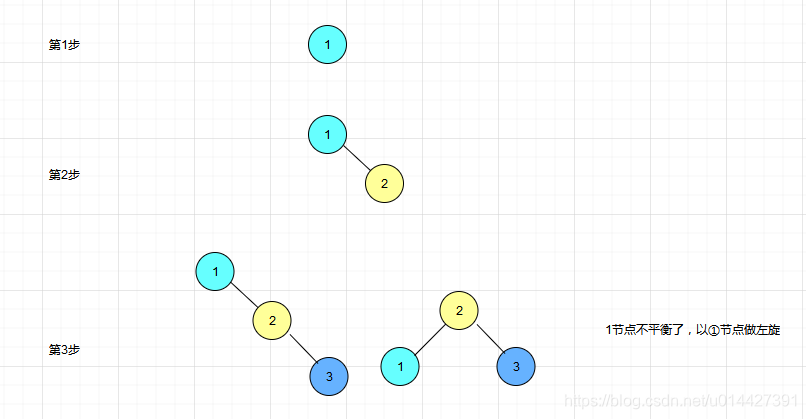
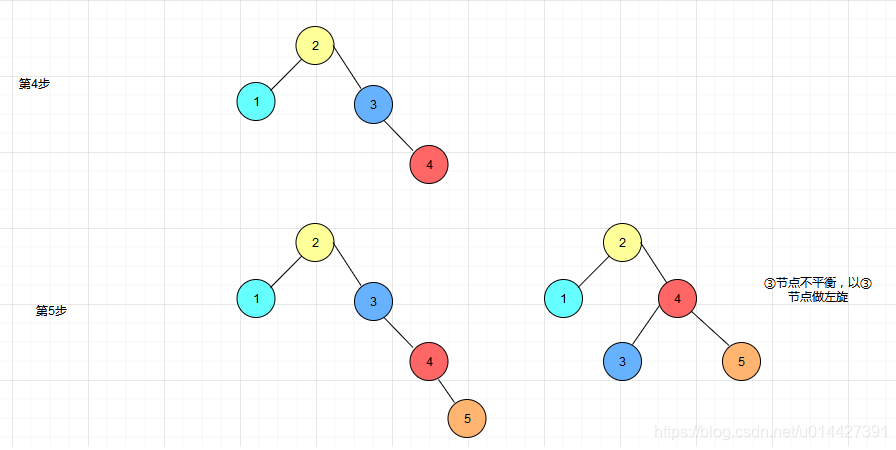
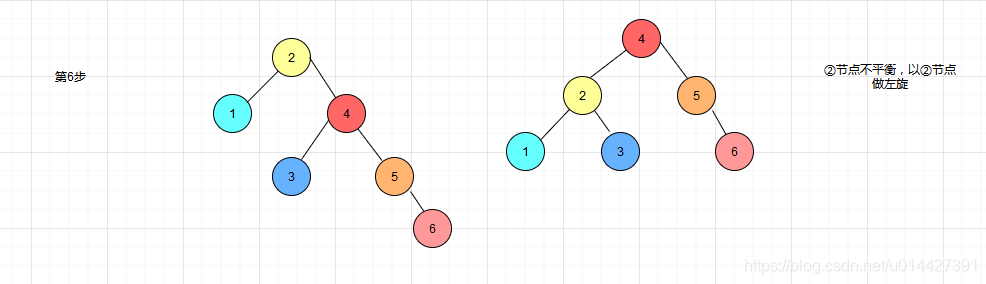
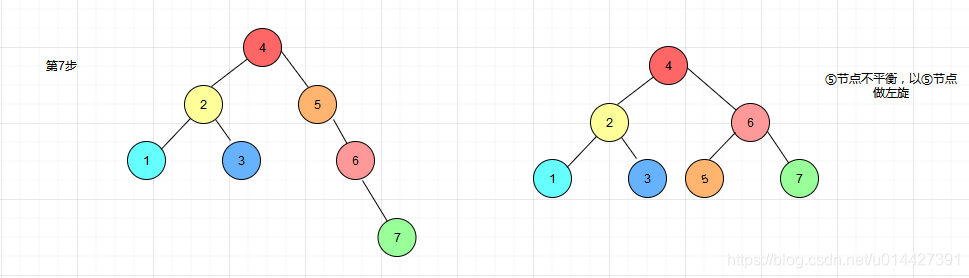
当然，可以通过https://www.cs.usfca.edu/~galles/visualization/AVLtree.html这个网站验证一遍

8、本文参考资料

• https://www.javadevjournal.com/data-structure/binary-tree-data-structure/

文章来源: smilenicky.blog.csdn.net，作者：smileNicky，版权归原作者所有，如需转载，请联系作者。

原文链接：smilenicky.blog.csdn.net/article/details/119417171