您在 Python 中迈入数据科学的第一步 |【生长吧!Python!】
目录
NumPy 是一个 Python 库,它提供了一个简单而强大的数据结构:n 维数组。这是构建 Python 数据科学工具包几乎所有功能的基础,学习 NumPy 是任何 Python 数据科学家旅程的第一步。本教程将为您提供使用 NumPy 和依赖它的更高级别库所需的知识。
在本教程中,您将学习:
- NumPy 使数据科学中的哪些核心概念成为可能
- 如何使用各种方法创建NumPy 数组
- 如何操作 NumPy 数组来执行有用的计算
- 如何将这些新技能应用于现实世界的问题
要充分利用本 NumPy 教程,您应该熟悉编写 Python 代码。完成Python 简介学习路径是确保您掌握基本技能的好方法。如果您熟悉矩阵数学,那么这也肯定会有所帮助。但是,您不需要了解任何有关数据科学的知识。你会在这里学到。
还有一个 NumPy 代码示例存储库,您将在本教程中看到。您可以将其用作参考并通过示例进行试验,以了解更改代码如何改变结果。
选择 NumPy:好处
由于您已经了解 Python,您可能会问自己是否真的需要学习一种全新的范式来进行数据科学。Python 的for循环很棒!读取和写入 CSV 文件可以使用传统代码完成。然而,学习新范式有一些令人信服的论据。
以下是 NumPy 可以为您的代码带来的四大好处:
- 速度更快: NumPy 使用 C 语言编写的算法,在纳秒而不是几秒内完成。
- 更少的循环: NumPy 可帮助您减少循环并避免在迭代索引中纠缠不清。
- 更清晰的代码:如果没有循环,您的代码看起来更像您要计算的方程式。
- 更好的质量:有成千上万的贡献者致力于保持 NumPy 的快速、友好和无错误。
由于这些好处,NumPy 是 Python 数据科学中多维数组的事实上的标准,许多最流行的库都建立在它之上。当您将知识扩展到数据科学的更具体领域时,学习 NumPy 是奠定坚实基础的好方法。
安装 NumPy
是时候设置所有内容了,这样您就可以开始学习如何使用 NumPy。有几种不同的方法可以做到这一点,按照NumPy 网站上的说明操作不会出错。但还有一些额外的细节需要注意,如下所述。
您还将安装Matplotlib。您将在后面的示例之一中使用它来探索其他库如何使用 NumPy。
使用 Repl.it 作为在线编辑器
如果您只是想开始一些示例,请按照本教程进行操作,并开始使用 NumPy 建立一些肌肉记忆,那么Repl.it是浏览器内编辑的绝佳选择。您可以在几分钟内注册并启动 Python 环境。在左侧,有一个包裹标签。您可以根据需要添加任意数量。对于本 NumPy 教程,请使用 NumPy 和 Matplotlib 的当前版本。
您可以在此处找到界面中的软件包:
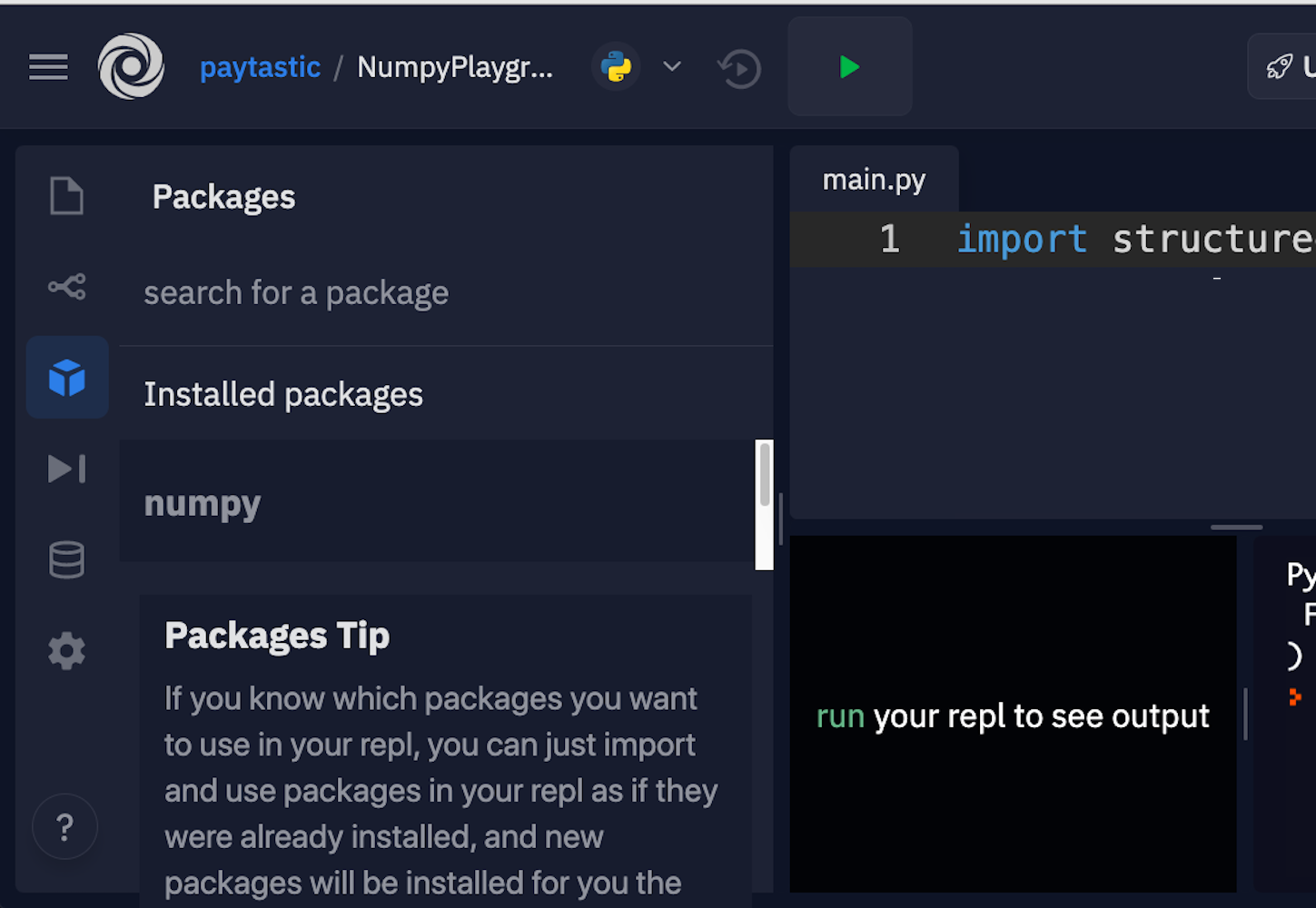
幸运的是,它们允许您单击并安装。
使用 Anaconda 安装 NumPy
该蟒蛇分布是围绕一个共同的捆绑Python数据科学工具套件包管理器,帮助管理您的虚拟环境和项目的依赖。它是围绕 构建的conda,它是实际的包管理器。这是 NumPy 项目推荐的方法,特别是如果您在尚未设置复杂开发环境的情况下使用 Python 进入数据科学。
如果您已经有一个喜欢使用的工作流pip、Pipenv、Poetry或其他一些工具集,那么最好不要添加conda到组合中。该conda软件包安装位置是分开的PyPI,和conda本身设置了一个独立的小岛包你的机器上,那么管理路径和记忆哪个包人的生活,可以是一个噩梦。
一旦你得到了已经conda安装完毕,就可以运行install了,你需要的库命令:
$ conda install numpy matplotlib这将安装本 NumPy 教程所需的内容,您就可以开始使用了。
安装 NumPy pip
尽管 NumPy 项目建议conda您在刚开始时使用,但您自己管理环境并仅使用 good old pip、Pipenv、Poetry 或任何其他您喜欢的替代品pip并没有错。
以下是用于设置的命令pip:
$ mkdir numpy-tutorial
$ cd numpy-tutorial
$ python3 -m venv .numpy-tutorial-venv
$ source .numpy-tutorial-venv/bin/activate
(.numpy-tutorial-venv)
$ pip install numpy matplotlib
Collecting numpy
Downloading numpy-1.19.1-cp38-cp38-macosx_10_9_x86_64.whl (15.3 MB)
|████████████████████████████████| 15.3 MB 2.7 MB/s
Collecting matplotlib
Downloading matplotlib-3.3.0-1-cp38-cp38-macosx_10_9_x86_64.whl (11.4 MB)
|████████████████████████████████| 11.4 MB 16.8 MB/s
...在此之后,请确保您的虚拟环境已激活,并且您的所有代码都应按预期运行。
使用 IPython、node或 JupyterLab
虽然上述部分应该为您提供入门所需的一切,但您可以选择安装更多工具,以使数据科学工作对开发人员更加友好。
IPython是升级的 Python读取-评估-打印循环 (REPL),它使在实时解释器会话中编辑代码更加直接和漂亮。下面是 IPython REPL 会话的样子:
In [1]: import numpy as np
In [2]: digits = np.array([
...: [1, 2, 3],
...: [4, 5, 6],
...: [6, 7, 9],
...: ])
In [3]: digits
Out[3]:
array([[1, 2, 3],
[4, 5, 6],
[6, 7, 9]])它与基本的 Python REPL 有几个不同之处,包括它的行号、颜色的使用和数组可视化的质量。还有很多用户体验奖励,让输入、重新输入和编辑代码变得更加愉快。
您可以独立安装 IPython:
$ pip install ipython或者,如果您等待并安装任何后续工具,那么它们将包含 IPython 的副本。
一个比 REPL 功能稍多一些的替代品是notebook。不过,Notebooks 的 Python 编写风格与标准脚本略有不同。它们不是传统的 Python 文件,而是为您提供一系列称为单元格的迷你脚本,您可以在同一个 Python 内存会话中以任何您想要的顺序运行和重新运行这些脚本。
笔记本的一个优点是你可以在单元格之间包含图表和呈现Markdown段落,因此它们非常适合在代码中编写数据分析!
这是它的样子:
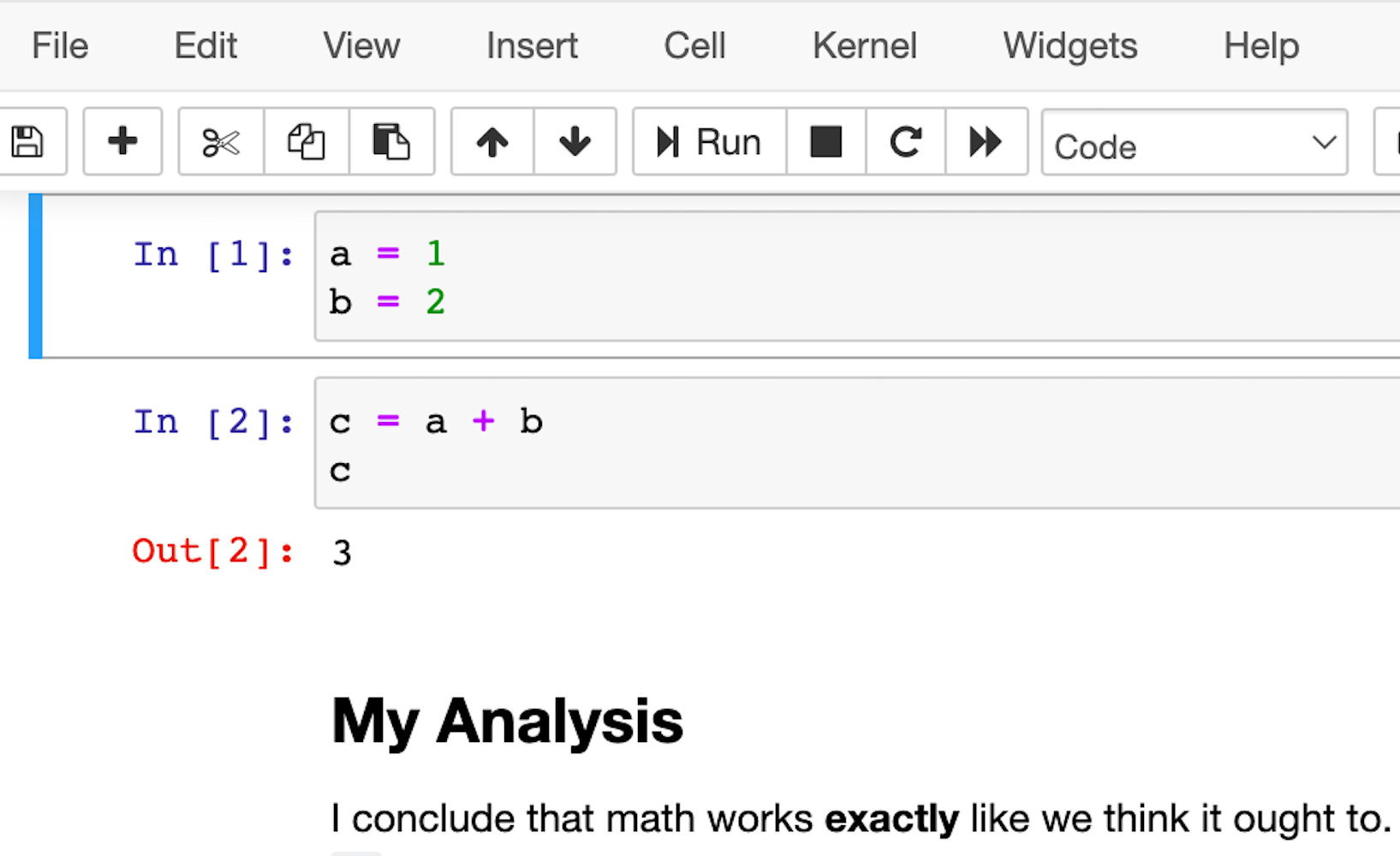
最流行的笔记本电脑产品可能是Jupyter笔记本电脑,但nteract是包裹Jupyter功能,并试图使其更有点平易近人和强大的另一种选择。
但是,如果您正在查看 Jupyter Notebook 并认为它需要更多类似 IDE 的品质,那么JupyterLab是另一种选择。您可以在基于浏览器的界面中自定义文本编辑器、笔记本、终端和自定义组件。对于来自MatLab 的人来说,它可能会更舒服。它是最年轻的产品,但它的 1.0 版本是在 2019 年发布的,所以它应该是稳定和完整的。
这是界面的样子:
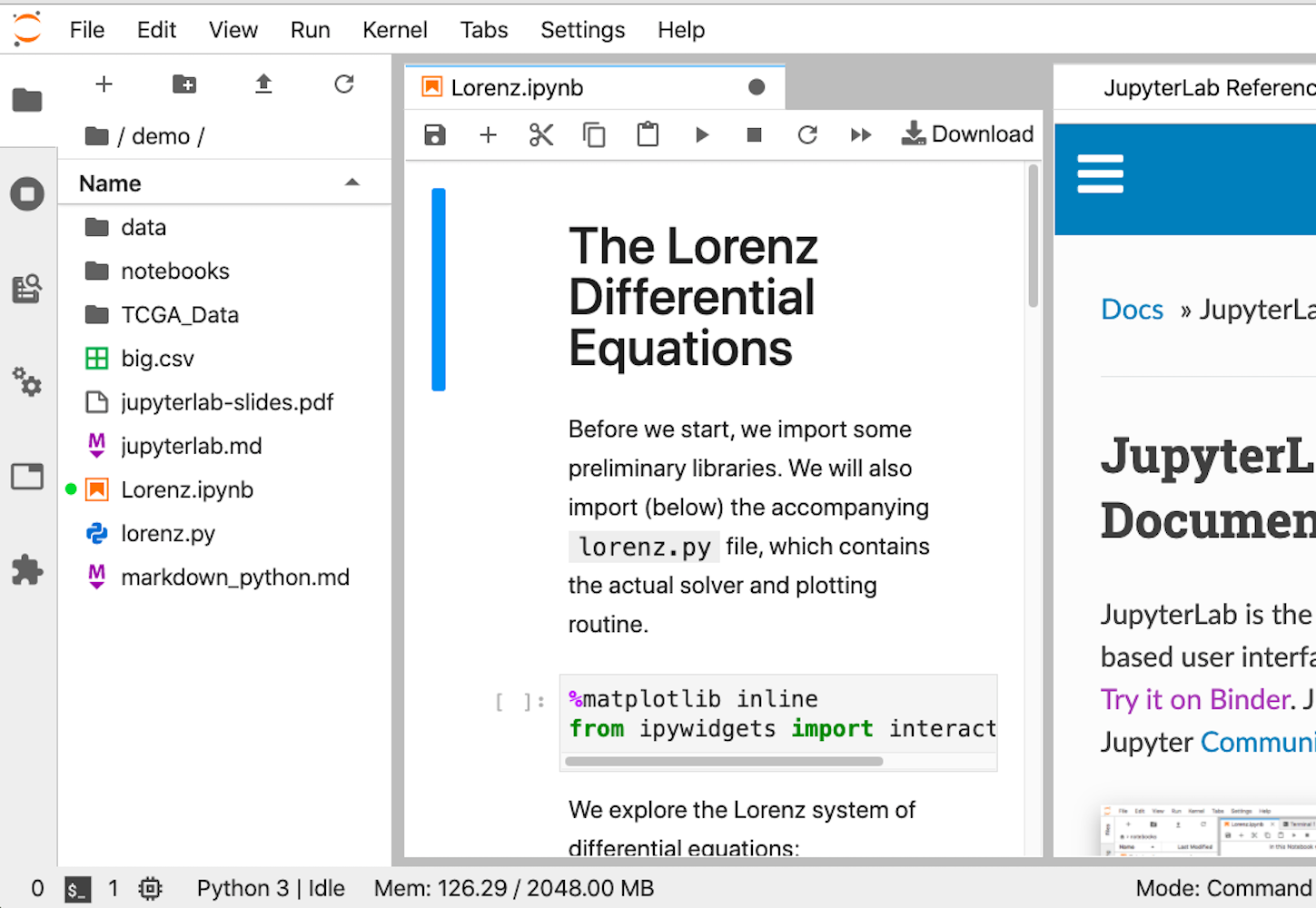
无论您选择哪个选项,一旦安装完成,您就可以开始运行 NumPy 代码的第一行了。现在是第一个例子的时候了。
Hello NumPy:弯曲测试成绩教程
第一个示例介绍了 NumPy 中的一些核心概念,您将在本教程的其余部分使用这些概念:
- 使用创建数组
numpy.array() - 像对待单个值一样处理完整的数组,使矢量化计算更具可读性
- 使用内置的 NumPy 函数来修改和聚合数据
这些概念是有效使用 NumPy 的核心。
场景是这样的:你是一名老师,刚刚在最近的一次考试中给你的学生评分。不幸的是,您可能让测试变得太具有挑战性,而且大多数学生的表现都比预期的要差。为了帮助大家了,你要去曲线大家的成绩。
不过,这将是一个相对基本的曲线。无论平均分数是多少,您都将获得 C。此外,您将确保曲线不会意外地损害学生的成绩或帮助学生取得超过 100% 的成绩。
将此代码输入到您的 REPL 中:
>>> import numpy as np
>>> CURVE_CENTER = 80
>>> grades = np.array([72, 35, 64, 88, 51, 90, 74, 12])
>>> def curve(grades):
... average = grades.mean()
... change = CURVE_CENTER - average
... new_grades = grades + change
... return np.clip(new_grades, grades, 100)
...
>>> curve(grades)
array([ 91.25, 54.25, 83.25, 100. , 70.25, 100. , 93.25, 31.25])原始分数已根据它们在包中的位置而增加,但没有一个超过 100%。
以下是重要的亮点:
- 第 1 行使用
np别名导入 NumPy ,这是一种常见的约定,可以为您节省一些击键次数。 - 第 3 行创建您的第一个 NumPy数组,它是一维的,形状为
(8,),数据类型为int64。不要太担心这些细节。您将在本教程的后面更详细地探索它们。 - 第 5 行使用取所有分数的平均值
.mean()。数组有很多的方法。
在第 7 行,您同时利用了两个重要概念:
- 矢量化
- 广播
向量化是以相同方式对数组中的每个元素执行相同操作的过程。这会for从您的代码中删除循环,但会获得相同的结果。
广播是扩展两个不同形状的数组并弄清楚如何在它们之间执行矢量化计算的过程。请记住,grades是形状数字的数组,(8,)并且change是标量或单个数字,本质上是形状(1,)。在这种情况下,NumPy 将标量添加到数组中的每个项目,并返回一个带有结果的新数组。
最后,在第 8 行,您将值限制或剪辑为一组最小值和最大值。除了数组方法,NumPy 还有大量的内置函数。您不需要全部记住它们——这就是文档的用途。任何时候你遇到困难或觉得应该有更简单的方法来做某事,看看文档,看看是否已经有一个例程可以完全满足你的需要。
在这种情况下,您需要一个接受数组并确保值不超过给定最小值或最大值的函数。clip()正是这样做的。
第 8 行还提供了另一个广播示例。对于 的第二个参数clip(),您通过grades,确保每个新弯曲的等级不会低于原始等级。但是对于第三个参数,您传递一个值:100。NumPy 获取该值并将其广播到 中的每个元素new_grades,确保没有一个新弯曲的成绩超过完美分数。
进入形状:阵列形状和轴
现在您已经了解了 NumPy 的一些功能,是时候用一些重要的理论来巩固这个基础了。有几个重要的概念需要牢记,尤其是在处理更高维度的数组时。
向量是一维数字数组,跟踪起来最简单。二维也不错,因为它们类似于电子表格。但是事情开始在三个维度上变得棘手,并且可视化四个维度?忘掉它。
掌握形状
当您使用多维数组时,形状是一个关键概念。在某个时候,更容易忘记将数据的形状可视化,而是遵循一些心理规则并相信 NumPy 会告诉您正确的形状。
所有数组都有一个称为.shape返回每个维度大小的元组的属性。哪个维度是哪个维度并不重要,但关键是您传递给函数的数组是函数期望的形状。确认您的数据具有正确形状的一种常用方法是打印数据及其形状,直到您确定一切都按预期工作。
下一个示例将展示此过程。您将创建一个具有复杂形状的数组,检查它并重新排序以使其看起来像它应该的样子:
In [1]: import numpy as np
In [2]: temperatures = np.array([
...: 29.3, 42.1, 18.8, 16.1, 38.0, 12.5,
...: 12.6, 49.9, 38.6, 31.3, 9.2, 22.2
...: ]).reshape(2, 2, 3)
In [3]: temperatures.shape
Out[3]: (2, 2, 3)
In [4]: temperatures
Out[4]:
array([[[29.3, 42.1, 18.8],
[16.1, 38. , 12.5]],
[[12.6, 49.9, 38.6],
[31.3, 9.2, 22.2]]])
In [5]: np.swapaxes(temperatures, 1, 2)
Out[5]:
array([[[29.3, 16.1],
[42.1, 38. ],
[18.8, 12.5]],
[[12.6, 31.3],
[49.9, 9.2],
[38.6, 22.2]]])在这里,您使用一个numpy.ndarray被调用的方法.reshape()来形成一个 2 × 2 × 3 的数据块。当您检查输入 3 中数组的形状时,它正是您告诉它的形状。但是,您可以看到打印的阵列如何迅速变得难以在三个或更多维度上进行可视化。与 交换轴后.swapaxes(),哪个维度是哪个维度就变得不太清楚了。您将在下一节中看到有关轴的更多信息。
形状将在广播部分再次出现。现在,请记住,这些小支票不需要任何费用。一旦事情顺利运行,您可以随时删除单元格或摆脱代码。
了解轴
上面的例子表明,不仅要知道数据的形状,还要知道哪些数据在哪个轴上是多么重要。在 NumPy 数组中,轴是零索引的并标识哪个维度是哪个。例如,一个二维数组有一个垂直轴(轴 0)和一个水平轴(轴 1)。NumPy 中的许多函数和命令会根据您告诉它们处理的轴来改变它们的行为。
此示例将显示.max()默认情况下的行为方式,没有axis参数,以及它如何根据axis您在提供参数时指定的内容来更改功能:
In [1]: import numpy as np
In [2]: table = np.array([
...: [5, 3, 7, 1],
...: [2, 6, 7 ,9],
...: [1, 1, 1, 1],
...: [4, 3, 2, 0],
...: ])
In [3]: table.max()
Out[3]: 9
In [4]: table.max(axis=0)
Out[4]: array([5, 6, 7, 9])
In [5]: table.max(axis=1)
Out[5]: array([7, 9, 1, 4])默认情况下,.max()无论有多少维,都返回整个数组中的最大值。但是,一旦您指定了一个轴,它就会对沿该特定轴的每组值执行该计算。例如,参数为axis=0,.max()选择 中四个垂直值集中的最大值,table并返回一个已展平或聚合为一维数组的数组。
事实上,许多 NumPy 的函数都是这样运行的:如果没有指定轴,则它们对整个数据集执行操作。否则,它们以轴向方式执行操作。
广播
到目前为止,您已经看到了几个较小的广播示例,但是您看到的示例越多,该主题将开始变得更有意义。从根本上说,它围绕一个规则运行:如果数组的维度匹配或其中一个数组的大小为1.
如果数组沿轴的大小匹配,则元素将逐个元素地进行操作,类似于内置 Python 函数的zip()工作方式。如果其中一个数组1在轴中的大小为,则该值将沿该轴广播,或者根据需要重复多次以匹配另一个数组中沿该轴的元素数。
这是一个快速示例。数组A有形状(4, 1, 8),数组B有形状(1, 6, 8)。根据上面的规则,你可以一起对这些数组进行操作:
- 在轴 0 中,
A有 a4和Ba1,因此B可以沿该轴广播。 - 在轴 1 中,
A有一个 1 和B一个 6,因此A可以沿该轴广播。 - 在轴 2 中,两个数组具有匹配的大小,因此它们可以成功运行。
所有三个轴都成功地遵循了规则。
您可以像这样设置数组:
In [1]: import numpy as np
In [2]: A = np.arange(32).reshape(4, 1, 8)
In [3]: A
Out[3]:
array([[[ 0, 1, 2, 3, 4, 5, 6, 7]],
[[ 8, 9, 10, 11, 12, 13, 14, 15]],
[[16, 17, 18, 19, 20, 21, 22, 23]],
[[24, 25, 26, 27, 28, 29, 30, 31]]])
In [4]: B = np.arange(48).reshape(1, 6, 8)
In [5]: B
Out[5]:
array([[[ 0, 1, 2, 3, 4, 5, 6, 7],
[ 8, 9, 10, 11, 12, 13, 14, 15],
[16, 17, 18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29, 30, 31],
[32, 33, 34, 35, 36, 37, 38, 39],
[40, 41, 42, 43, 44, 45, 46, 47]]])A有4平面,每个平面都有1行和8列。B只有1带有6行和8列的平面。当您尝试在它们之间进行计算时,看看 NumPy 为您做了什么!
将两个数组相加:
In [7]: A + B
Out[7]:
array([[[ 0, 2, 4, 6, 8, 10, 12, 14],
[ 8, 10, 12, 14, 16, 18, 20, 22],
[16, 18, 20, 22, 24, 26, 28, 30],
[24, 26, 28, 30, 32, 34, 36, 38],
[32, 34, 36, 38, 40, 42, 44, 46],
[40, 42, 44, 46, 48, 50, 52, 54]],
[[ 8, 10, 12, 14, 16, 18, 20, 22],
[16, 18, 20, 22, 24, 26, 28, 30],
[24, 26, 28, 30, 32, 34, 36, 38],
[32, 34, 36, 38, 40, 42, 44, 46],
[40, 42, 44, 46, 48, 50, 52, 54],
[48, 50, 52, 54, 56, 58, 60, 62]],
[[16, 18, 20, 22, 24, 26, 28, 30],
[24, 26, 28, 30, 32, 34, 36, 38],
[32, 34, 36, 38, 40, 42, 44, 46],
[40, 42, 44, 46, 48, 50, 52, 54],
[48, 50, 52, 54, 56, 58, 60, 62],
[56, 58, 60, 62, 64, 66, 68, 70]],
[[24, 26, 28, 30, 32, 34, 36, 38],
[32, 34, 36, 38, 40, 42, 44, 46],
[40, 42, 44, 46, 48, 50, 52, 54],
[48, 50, 52, 54, 56, 58, 60, 62],
[56, 58, 60, 62, 64, 66, 68, 70],
[64, 66, 68, 70, 72, 74, 76, 78]]])广播的工作方式是 NumPy 将平面复制B3 次,因此总共有 4 个,与A. 它还将单行复制A五次,总共六次,与 中的行数相匹配B。然后它将新扩展A数组中的每个元素添加到B. 每个计算的结果显示在输出的相应位置。
注意:这是使用arange()!从范围创建数组的好方法!
再一次,即使您可以使用“平面”、“行”和“列”等词来描述如何广播此示例中的形状以创建匹配的 3D 形状,但在更高维度上情况会变得更加复杂。很多时候,您必须简单地遵循广播规则并进行大量打印以确保事情按计划进行。
了解广播是掌握矢量化计算的重要部分,而矢量化计算是编写干净、惯用的 NumPy 代码的方式。
数据科学操作:过滤、排序、聚合
这部分在理论上很重,但对实际的、现实世界的例子来说有点轻。在本节中,您将学习一些真实有用的数据科学操作示例:过滤、排序和聚合数据。
索引
索引使用许多与普通 Python 代码相同的习语。您可以使用正或负索引从数组的前面或后面进行索引。您可以使用冒号 ( :) 来指定“其余部分”或“全部”,您甚至可以使用两个冒号来跳过与常规 Python 列表一样的元素。
区别如下:NumPy 数组在轴之间使用逗号,因此您可以在一组方括号中索引多个轴。一个例子是展示这一点的最简单方法。是时候确认丢勒魔方了!
下面的数字方块有一些惊人的特性。如果您将任何行、列或对角线相加,您将得到相同的数字,即 34。如果您将四个象限、中心的四个正方形、四个角的每一个相加,您也会得到同样的数字正方形,或任何包含的 3 × 3 网格的四个角正方形。你要证明!
有趣的事实:在底行,数字 15 和 14 位于中间,代表丢勒创建这个正方形的年份。数字 1 和 4 也在该行,代表字母表的第一个和第四个字母 A 和 D,它们是正方形创建者 Albrecht Dürer 的首字母!
在您的 REPL 中输入以下内容:
In [1]: import numpy as np
In [2]: square = np.array([
...: [16, 3, 2, 13],
...: [5, 10, 11, 8],
...: [9, 6, 7, 12],
...: [4, 15, 14, 1]
...: ])
In [3]: for i in range(4):
...: assert square[:, i].sum() == 34
...: assert square[i, :].sum() == 34
...:
In [4]: assert square[:2, :2].sum() == 34
In [5]: assert square[2:, :2].sum() == 34
In [6]: assert square[:2, 2:].sum() == 34
In [7]: assert square[2:, 2:].sum() == 34在for循环内部,您验证所有行和所有列的总和为 34。之后,使用选择性索引,您验证每个象限的总和也为 34。
最后要注意的一件事是,您可以将任何数组的总和与square.sum(). 此方法也可以采用axis参数来进行轴向求和。
屏蔽和过滤
基于索引的选择很棒,但是如果您想根据更复杂的非均匀或非顺序标准过滤数据怎么办?这就是面具的概念发挥作用的地方。
掩模是具有完全相同的形状作为数据数组,但不是您的值,它保存布尔值:要么True或False。您可以使用此掩码数组以非线性和复杂的方式索引数据数组。它将返回布尔数组具有True值的所有元素。
这是一个显示该过程的示例,首先是慢动作,然后是通常如何完成,全部在一行中:
In [1]: import numpy as np
In [2]: numbers = np.linspace(5, 50, 24, dtype=int).reshape(4, -1)
In [3]: numbers
Out[3]:
array([[ 5, 6, 8, 10, 12, 14],
[16, 18, 20, 22, 24, 26],
[28, 30, 32, 34, 36, 38],
[40, 42, 44, 46, 48, 50]])
In [4]: mask = numbers % 4 == 0
In [5]: mask
Out[5]:
array([[False, False, True, False, True, False],
[ True, False, True, False, True, False],
[ True, False, True, False, True, False],
[ True, False, True, False, True, False]])
In [6]: numbers[mask]
Out[6]: array([ 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48])
In [7]: by_four = numbers[numbers % 4 == 0]
In [8]: by_four
Out[8]: array([ 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48])稍后您将在输入 2 中看到对新数组创建技巧的解释,但现在,请关注示例的重点。这些是重要的部分:
- 输入 4通过执行向量化布尔计算来创建掩码,获取每个元素并检查它是否被 4 整除。这将返回一个具有相同形状的掩码数组,其中包含计算的元素结果。
- 输入 6使用此掩码来索引原始
numbers数组。这会导致数组失去其原始形状,将其缩小为一维,但您仍然可以获得所需的数据。 - 输入 7提供了一个更传统的、惯用的掩码选择,您可能会在野外看到,并在选择括号内内联创建匿名过滤数组。此语法类似于 R 编程语言中的用法。
回到输入 2,您会遇到三个新概念:
- 使用
np.linspace(),以产生均匀间隔的阵列 - 设置
dtype输出 - 用
-1
np.linspace()生成在最小值和最大值之间均匀分布的n 个数字,这对于科学绘图中的均匀分布采样很有用。
因为本示例中的特定计算的,它使生活更容易有整数中numbers阵列。但是因为 5 和 50 之间的空间不能被 24 整除,所以结果数字将是浮点数。您指定 a dtypeofint以强制函数向下舍入并为您提供整数。稍后您将看到有关数据类型的更详细讨论。
最后,array.reshape()可以将其-1作为其维度大小之一。这意味着 NumPy 应该根据其他轴的大小来确定该特定轴需要多大。在这种情况下,轴 0 中的24值和大小为4,轴 1 的大小为6。
这里还有一个例子来展示掩码过滤的威力。的正态分布是其中值大约95.45%发生两种内的概率分布的标准偏差的平均值的。
您可以通过 NumPyrandom生成随机值的模块的一些帮助来验证:
In [1]: import numpy as np
In [2]: from numpy.random import default_rng
In [3]: rng = default_rng()
In [4]: values = rng.standard_normal(10000)
In [5]: values[:5]
Out[5]: array([ .9779210858, 1.8361585253, -.3641365235,
-.1311344527, 1.286542056 ])
In [6]: std = values.std()
In [7]: std
Out[7]: .9940375551073492
In [8]: filtered = values[(values > -2 * std) & (values < 2 * std)]
In [9]: filtered.size
Out[9]: 9565
In [10]: values.size
Out[10]: 10000
In [11]: filtered.size / values.size
Out[11]: 0.9565在这里,您使用了一种可能看起来很奇怪的语法来组合过滤条件:二元&运算符。为什么会是这样?这是因为 NumPy 指定&和|作为向量化的、按元素的运算符来组合布尔值。如果您尝试这样做A and B,那么您将收到有关数组的真值如何奇怪的警告,因为and正在对整个数组的真值进行操作,而不是逐个元素。
转置、排序和连接
其他操作虽然不像索引或过滤那样常见,但也可能非常方便,具体取决于您所处的情况。您将在本节中看到一些示例。
这是转置数组:
In [1]: import numpy as np
In [2]: a = np.array([
...: [1, 2],
...: [3, 4],
...: [5, 6],
...: ])
In [3]: a.T
Out[3]:
array([[1, 3, 5],
[2, 4, 6]])
In [4]: a.transpose()
Out[4]:
array([[1, 3, 5],
[2, 4, 6]])当您计算数组的转置时,每个元素的行和列索引都会切换。[0, 2]例如,Item变为 item [2, 0]。您还可以a.T用作a.transpose().
以下代码块显示了排序,但您还将在接下来的结构化数据部分中看到更强大的排序技术:
In [1]: import numpy as np
In [2]: data = np.array([
...: [7, 1, 4],
...: [8, 6, 5],
...: [1, 2, 3]
...: ])
In [3]: np.sort(data)
Out[3]:
array([[1, 4, 7],
[5, 6, 8],
[1, 2, 3]])
In [4]: np.sort(data, axis=None)
Out[4]: array([1, 1, 2, 3, 4, 5, 6, 7, 8])
In [5]: np.sort(data, axis=0)
Out[5]:
array([[1, 1, 3],
[7, 2, 4],
[8, 6, 5]])省略axis参数会自动选择最后一个和最里面的维度,即本示例中的行。使用展None平数组并执行全局排序。否则,您可以指定所需的轴。在输出 5 中,数组的每一列仍然具有其所有元素,但它们已在该列内从低到高排序。
最后,这里有一个concatenation的例子。虽然有一个np.concatenate()函数,但也有一些辅助函数有时更容易阅读。
这里有些例子:
In [1]: import numpy as np
In [2]: a = np.array([
...: [4, 8],
...: [6, 1]
...: ])
In [3]: b = np.array([
...: [3, 5],
...: [7, 2],
...: ])
In [4]: np.hstack((a, b))
Out[4]:
array([[4, 8, 3, 5],
[6, 1, 7, 2]])
In [5]: np.vstack((b, a))
Out[5]:
array([[3, 5],
[7, 2],
[4, 8],
[6, 1]])
In [6]: np.concatenate((a, b))
Out[6]:
array([[4, 8],
[6, 1],
[3, 5],
[7, 2]])
In [7]: np.concatenate((a, b), axis=None)
Out[7]: array([4, 8, 6, 1, 3, 5, 7, 2])输入 4 和 5 显示稍微更直观的功能hstack()和vstack()。输入 6 和 7 显示更通用concatenate(),首先没有axis参数,然后有axis=None。这种扁平化行为在形式上与您刚刚看到的sort().
需要注意的一个重要绊脚石是所有这些函数都将数组元组作为它们的第一个参数,而不是您可能期望的可变数量的参数。您可以分辨出来,因为有一对额外的括号。
聚合
在深入研究一些更高级的主题和示例之前,本次功能之旅的最后一站是聚合。你已经看到了不少聚集的方法,其中包括.sum(),.max(),.mean(),和.std()。您可以参考 NumPy 更大的函数库以查看更多信息。许多数学、金融和统计函数使用聚合来帮助您减少数据中的维数。
实际示例 1:实现麦克劳林级数
现在是时候查看上述部分中介绍的技能的实际用例了:实现方程。
在没有 NumPy 的情况下将数学方程转换为代码的最困难的事情之一是缺少许多视觉相似性,这使得在阅读代码时很难分辨出你正在查看方程的哪个部分。求和被转换为更详细的for循环,并且限制优化最终看起来像while循环。
使用 NumPy 可以让您更接近从方程到代码的一对一表示。
在下一个示例中,您将对e x的麦克劳林级数进行编码。麦克劳林级数是一种用以零为中心的无限求和项级数逼近更复杂函数的方法。
对于e x,麦克劳林级数是以下总和:
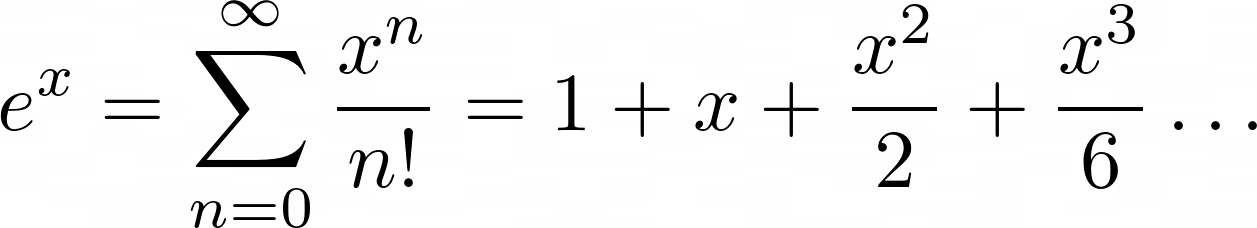
您将项从零开始加起来,理论上到无穷大。每个第n项将x升至n并除以n!,这是阶乘运算的表示法。
现在是您将其放入 NumPy 代码的时候了。创建一个名为 的文件maclaurin.py:
from math import e, factorial
import numpy as np
fac = np.vectorize(factorial)
def e_x(x, terms=10):
"""Approximates e^x using a given number of terms of
the Maclaurin series
"""
n = np.arange(terms)
return np.sum((x ** n) / fac(n))
if __name__ == "__main__":
print("Actual:", e ** 3) # Using e from the standard library
print("N (terms)\tMaclaurin\tError")
for n in range(1, 14):
maclaurin = e_x(3, terms=n)
print(f"{n}\t\t{maclaurin:.03f}\t\t{e**3 - maclaurin:.03f}")运行此程序时,您应该看到以下结果:
$ python3 maclaurin.py
Actual: 20.085536923187664
N (terms) Maclaurin Error
1 1.000 19.086
2 4.000 16.086
3 8.500 11.586
4 13.000 7.086
5 16.375 3.711
6 18.400 1.686
7 19.412 0.673
8 19.846 0.239
9 20.009 0.076
10 20.063 0.022
11 20.080 0.006
12 20.084 0.001
13 20.085 0.000随着您增加项数,您的麦克劳林值越来越接近实际值,您的误差也越来越小。
每个项的计算涉及取x到n的功率和通过分割n!,或阶乘的n。加法、求和和求幂都是 NumPy 可以自动快速矢量化的操作,但对于factorial().
要factorial()在矢量化计算中使用,您必须使用np.vectorize()来创建矢量化版本。的文档np.vectorize()说明它只不过是一个将for循环应用于给定函数的薄包装器。使用它代替普通的 Python 代码并没有真正的性能优势,并且可能会有一些开销损失。然而,正如您稍后将看到的,可读性优势是巨大的。
一旦您的向量化阶乘就位,计算整个麦克劳林级数的实际代码就会非常短。它也是可读的。最重要的是,它与数学方程的外观几乎完全一一对应:
n = np.arange(terms)
return np.sum((x ** n) / fac(n))这是一个非常重要的想法,值得重复。除了要 initialize 的额外行外n,代码的读法几乎与原始数学方程完全相同。没有for循环,没有临时i, j, k变量。简单明了,数学。
就像那样,您正在使用 NumPy 进行数学编程!如需额外练习,请尝试选择其他 Maclaurin 系列之一并以类似方式实施。
优化存储:数据类型
现在您有了更多的实践经验,是时候回到理论并研究数据类型了。数据类型在很多 Python 代码中并没有发挥核心作用。数字按预期工作,字符串做其他事情,布尔值是真或假,除此之外,您可以创建自己的对象和集合。
但是,在 NumPy 中,还有更多细节需要涵盖。NumPy 在底层使用 C 代码来优化性能,除非数组中的所有项都属于同一类型,否则它无法做到这一点。这不仅仅意味着相同的 Python 类型。它们必须是相同的底层 C 类型,具有相同的形状和大小(以位为单位)!
数值类型:int,bool,float,和complex
由于您的大多数数据科学和数值计算都倾向于涉及数字,因此它们似乎是最好的起点。NumPy 代码中基本上有四种数字类型,每一种都可以采用几种不同的大小。
下表细分了这些类型的详细信息:
| Name | 位数 | Python 类型 | NumPy 类型 |
|---|---|---|---|
| 整数 | 64 | int |
np.int_ |
| 布尔值 | 8 | bool |
np.bool_ |
| 漂浮 | 64 | float |
np.float_ |
| 复杂的 | 128 | complex |
np.complex_ |
这些只是映射到现有 Python 类型的类型。NumPy 还具有每个较小版本的类型,例如 8 位、16 位和 32 位整数、32 位单精度浮点数和 64 位单精度复数。该文件列出了他们的全部。
要在创建数组时指定类型,您可以提供一个dtype参数:
In [1]: import numpy as np
In [2]: a = np.array([1, 3, 5.5, 7.7, 9.2], dtype=np.single)
In [3]: a
Out[3]: array([1. , 3. , 5.5, 7.7, 9.2], dtype=float32)
In [4]: b = np.array([1, 3, 5.5, 7.7, 9.2], dtype=np.uint8)
In [5]: b
Out[5]: array([1, 3, 5, 7, 9], dtype=uint8)NumPy 会自动将您的平台无关类型转换np.single为您的平台支持该大小的任何固定大小类型。在这种情况下,它使用np.float32. 如果您提供的值与您提供的形状不匹配dtype,那么 NumPy 将为您修复它或引发错误。
字符串类型:大小的 Unicode
字符串在 NumPy 代码中的行为有点奇怪,因为 NumPy 需要知道预期的字节数,这在 Python 编程中通常不是一个因素。幸运的是,NumPy 在为您处理不太复杂的情况方面做得非常好:
In [1]: import numpy as np
In [2]: names = np.array(["bob", "amy", "han"], dtype=str)
In [3]: names
Out[3]: array(['bob', 'amy', 'han'], dtype='<U3')
In [4]: names.itemsize
Out[4]: 12
In [5]: names = np.array(["bob", "amy", "han"])
In [6]: names
Out[6]: array(['bob', 'amy', 'han'], dtype='<U3')
In [7]: more_names = np.array(["bobo", "jehosephat"])
In [8]: np.concatenate((names, more_names))
Out[8]: array(['bob', 'amy', 'han', 'bobo', 'jehosephat'], dtype='<U10')在输入 2 中,您提供了dtypePython 的内置str类型,但在输出 3 中,它已转换为大小为 的小端 Unicode字符串3。当您检查输入 4 中给定项的大小时,您会看到它们每个12字节:三个 4 字节 Unicode 字符。
注意:在处理 NumPy 数据类型时,您必须考虑诸如值的字节顺序之类的事情。在这种情况下,这dtype '<U3'意味着每个值都是三个 Unicode 字符的大小,最低有效字节首先存储在内存中,最高有效字节存储在最后。A dtypeof'>U3'表示相反。
作为一个例子,表示NumPy的Unicode字符“🐍”与字节0xF4 0x01 0x00用dtype的'<U1'和0x00 0x01 0xF4用dtype的'>U1'。通过创建一个充满表情符号的数组来尝试一下,将 设置dtype为一个或另一个,然后调用.tobytes()您的数组!
如果您想研究 Python 如何处理普通 Python 数据类型的 1 和 0,那么struct library的官方文档是另一个很好的资源,它是一个使用原始字节的标准库模块。
当您将它与具有更大项目的数组结合以在输入 8 中创建一个新数组时,NumPy 会帮助计算出新数组的项目需要有多大并将它们全部增长到 size <U10。
但是当您尝试修改其中一个插槽的值大于 容量时会发生以下情况dtype:
In [9]: names[2] = "jamima"
In [10]: names
Out[10]: array(['bob', 'amy', 'jam'], dtype='<U3')它没有按预期工作,而是截断了您的价值。如果您已经有一个数组,那么 NumPy 的自动大小检测将不适合您。你得到三个字符,就是这样。其余的消失在虚空中。
这就是说,一般来说,当您处理字符串时,NumPy 会支持您,但您应该始终注意元素的大小,并确保在修改或更改数组时有足够的空间。
结构化数组
最初,您了解到数组项都必须是相同的数据类型,但这并不完全正确。NumPy 有一种特殊的数组,称为记录数组或结构化数组,您可以使用它指定类型,并且可以选择按列指定名称。这使得排序和过滤功能更加强大,感觉类似于在Excel、CSV或关系数据库中处理数据。
这是一个快速示例,可以稍微展示一下:
In [1]: import numpy as np
In [2]: data = np.array([
...: ("joe", 32, 6),
...: ("mary", 15, 20),
...: ("felipe", 80, 100),
...: ("beyonce", 38, 9001),
...: ], dtype=[("name", str, 10), ("age", int), ("power", int)])
In [3]: data[0]
Out[3]: ('joe', 32, 6)
In [4]: data["name"]
Out[4]: array(['joe', 'mary', 'felipe', 'beyonce'], dtype='<U10')
In [5]: data[data["power"] > 9000]["name"]
Out[5]: array(['beyonce'], dtype='<U10')在输入 2 中,您创建了一个数组,但每个项目都是一个具有名称、年龄和功率级别的元组。对于dtype,你实际上提供关于每个字段的信息元组的列表:name为10个字符的Unicode的领域,都age和power是标准的4字节或8字节的整数。
在输入 3 中,您可以看到称为记录的行仍然可以使用索引访问。
在输入 4 中,您会看到用于访问整个列或字段的新语法。
最后,在输入 5 中,您会看到基于字段和基于字段的选择的基于掩码的过滤的超强大组合。请注意阅读以下SQL查询并没有太大的不同:
SELECT name FROM data
WHERE power > 9000;在这两种情况下,结果都是功率级别超过的名称列表9000。
您甚至可以ORDER BY通过使用以下功能来添加功能np.sort():
In [6]: np.sort(data[data["age"] > 20], order="power")["name"]
Out[6]: array(['joe', 'felipe', 'beyonce'], dtype='<U10')这会power在检索数据之前对数据进行排序,这完善了您选择、过滤和排序项目的 NumPy 工具,就像您在 SQL 中所做的一样!
更多关于数据类型
本教程的这一部分旨在让您获得足够的知识来提高 NumPy 的数据类型的工作效率,了解一些底层的工作原理,并认识到一些常见的陷阱。这当然不是详尽的指南。在对NumPy的文档ndarrays有万吨以上的资源。
还有更多关于dtype对象的信息,包括构造、定制和优化它们的不同方法,以及如何使它们更健壮地满足您的所有数据处理需求。如果您遇到麻烦并且您的数据没有完全按照您的预期加载到数组中,那么这是一个很好的起点。
最后,NumPyrecarray本身就是一个强大的对象,您实际上只是触及了结构化数据集功能的皮毛。绝对值得通读recarray文档以及NumPy 提供的其他专用数组子类的文档。
展望未来:更强大的库
在下一节中,您将继续学习建立在上面看到的基本构建块之上的强大工具。以下是您在全面掌握 Python 数据科学的道路上的下一步需要考虑的一些库。
pandas
pandas是一个库,它采用结构化数组的概念,并使用大量方便的方法、开发人员体验改进和更好的自动化来构建它。如果你需要从基本上任何地方导入数据,清理它,重塑它,打磨它,然后将它导出成任何格式,那么pandas就是你的库。这可能是因为在某些时候,你会import pandas as pd在同一时间你import numpy as np。
pandas 文档有一个快速教程,里面有很多具体的例子,叫做10 Minutes to pandas。这是一个很好的资源,您可以使用它来进行一些快速的动手练习。
scikit 学习
如果您的目标更倾向于机器学习,那么下一步就是scikit-learn。给定足够的数据,您可以在短短几行中进行分类、回归、聚类等操作。
如果您已经熟悉数学,那么 scikit-learn 文档中有很多教程可以让您在 Python 中上手和运行。如果没有,那么数据科学学习路径的数学是一个很好的起点。此外,还有一个完整的机器学习学习路径。
重要的是您至少要了解算法背后的数学基础,而不仅仅是导入它们并使用它运行。机器学习模型中的偏见是一个巨大的伦理、社会和政治问题。
在不考虑如何解决偏见的情况下将数据扔给模型是陷入困境并对人们的生活产生负面影响的好方法。做一些研究并学习如何预测可能发生偏见的地方是朝着正确方向迈出的良好开端。
Matplotlib
无论您对数据做什么,在某些时候您都需要将您的结果传达给其他人,而Matplotlib是实现这一目标的主要库之一。有关介绍,请查看使用 Matplotlib 绘图。在下一节中,您将获得一些使用 Matplotlib 的动手练习,但您将使用它来处理图像而不是制作绘图。
实际示例 2:使用 Matplotlib 操作图像
当您使用 Python 库时,它总是很整洁,并且它会为您提供一些事实证明是基本 NumPy 数组的东西。在此示例中,您将体验到它的所有荣耀。
您将使用 Matplotlib 加载图像,意识到 RGB 图像实际上只是整数width × height × 3数组int8,操作这些字节,并在完成后再次使用 Matplotlib 保存修改后的图像。
下载此图像以使用:

这是一张 1920 x 1299 像素的可爱小猫图片。您将更改这些像素的颜色。
创建一个名为 的 Python 文件image_mod.py,然后设置导入并加载图像:
import numpy as np
import matplotlib.image as mpimg
img = mpimg.imread("kitty.jpg")
print(type(img))
print(img.shape)这是一个好的开始。Matplotlib 有自己的图像处理模块,您将依赖它,因为它可以直接读取和写入图像格式。
如果您运行此代码,那么您的朋友 NumPy 数组将出现在输出中:
$ python3 image_mod.py
<class 'numpy.ndarray'>
(1299, 1920, 3)这是一张高度为 1299 像素、宽度为 1920 像素和三个通道的图像:红色、绿色和蓝色 (RGB) 颜色级别各一个。
想看看当你退出 R 和 G 通道时会发生什么吗?将此添加到您的脚本中:
output = img.copy() # The original image is read-only!
output[:, :, :2] = 0
mpimg.imsave("blue.jpg", output)再次运行并检查文件夹。应该有一个新图像:

你脑子进水了吗?你感受到力量了吗?图像只是花哨的数组!像素只是数字!
但是现在,是时候做一些更有用的事情了。您要将此图像转换为灰度。但是,转换为灰度更复杂。平均 R、G 和 B 通道并使它们全部相同将为您提供灰度图像。但是人类的大脑很奇怪,这种转换似乎并不能很好地处理颜色的亮度。
其实还是自己看比较好。您可以使用这样一个事实:如果您输出一个只有一个通道而不是三个通道的数组,那么您可以指定一个颜色图,cmap在 Matplotlib 世界中称为 a 。如果您指定 a cmap,则 Matplotlib 将为您处理线性梯度计算。
删除脚本中的最后三行并将它们替换为:
averages = img.mean(axis=2) # Take the average of each R, G, and B
mpimg.imsave("bad-gray.jpg", averages, cmap="gray")这些新行创建了一个名为 的新数组averages,它是img您通过取所有三个通道的平均值沿轴 2 展平的数组的副本。您已对所有三个通道求平均值,并输出了 R、G 和 B 值等于该平均值的值。当 R、G 和 B 都相同时,结果颜色在灰度上。
它最终产生的结果并不可怕:

但是您可以使用亮度方法做得更好。这种技术对三个通道进行加权平均,认为绿色驱动图像看起来有多亮,蓝色可以使它看起来更暗。您将使用@运算符,它是 NumPy 的运算符,用于执行传统的二维数组点积。
再次替换脚本中的最后两行:
weights = np.array([0.3, 0.59, 0.11])
grayscale = img @ weights
mpimg.imsave("good-gray.jpg", grayscale, cmap="gray")这一次,您将完成一个dot product,而不是做一个平坦的平均值,它是三个值的一种加权组合。由于权重加起来为 1,它完全等同于对三个颜色通道进行加权平均。
结果如下:

第一张图像有点暗,边缘和阴影更粗。第二张图像更亮更亮,暗线没有那么粗。你有它 - 你使用 Matplotlib 和 NumPy 数组来操作图像!
结论
无论您的数据处于多少维度,NumPy 都为您提供了使用它的工具。你可以存储它、重塑它、组合它、过滤它和排序它,你的代码读起来就像你一次只操作一个数字,而不是数百或数千。
在本教程中,您学习了:
- NumPy 使数据科学的核心概念成为可能
- 如何使用各种方法创建NumPy 数组
- 如何操作 NumPy 数组来执行有用的计算
- 如何将这些新技能应用于现实世界的问题
不要忘记查看本教程中 NumPy 代码示例的存储库。您可以将其用作参考并通过示例进行试验,以了解更改代码如何改变结果:
【生长吧!Python】有奖征文火热进行中:https://bbs.huaweicloud.cn/blogs/278897
- 点赞
- 收藏
- 关注作者


评论(0)